Trigonometry NTSE & JEE Foundation | Class 10 Solved Problems and Examples

ANAND CLASSES Study Material and Notes to Master Trigonometry with solved problems and examples designed for NTSE and JEE Foundation students. Strengthen your concepts with step-by-step solutions.

Trigonometry Practical Solved Problems for NTSE & JEE Foundation Exams

If sin A + cosec A = 2; Find the value of sin² A + cosec² A.

Solution:

Given, sin A + cosec A = 2

On squaring on both sides, we have

(sin A + cosec A)² = 2²

sin² A + cosec² A + 2sinA. cosec A = 4

sin² A + cosec² A + 2 = 4 [As sin A. cosec A = sin A x 1/sin A = 1]

sin² A + cosec² A = 4 – 2 = 2

Hence, the value of (sin² A + cosec² A) is 2

Evaluate the values of: (i) cos B (ii) sec² B (ii) cot C (iii) sin²B + cos²B (iv) sin B. cos C + cos B. sin C from the following diagram.

Solution:

Given that, ∠BAC = 90^o

BC² = AB² + AC² (From diagram, BC is the hypotenuse)

17² = 8² + AC²

AC² = 289 – 64 = 225

Taking square root on both sides, we get

AC = 15 cm

(i) cos B = base/hypotenuse

cos B = AB/BC = 8/17

(ii) sec² B = (hypotenuse/base)²

sec² B = (BC/AB)² = (17/8)² = 289/64

(iii) cot C = base/perpendicular

cot C = AC/AB = 15/8

(iii) sin B = perpendicular/hypotenuse

sin B = AC/BC = 15/17

cos B = base/hypotenuse

cos B = AB/BC = 8/17

Now,

sin² B + cos² B = (15/17)² + (8/17)²

sin² B + cos² B = (225 + 64)/289 = 289/289 = 1

(iv) sin B = perpendicular/hypotenuse

sin B = AC/BC = 15/17

cos B = base/hypotenuse

cos B = AB/BC = 8/17

sin C = perpendicular/hypotenuse

sin C = AB/BC = 8/17

cos C = base/hypotenuse

cos C = AC/BC = 15/17

Now,

sin B. cos C + cos B. sin C = 15/17 x 15/17 + 8/17 x 8/17

sin B. cos C + cos B. sin C = (225 + 64)/289

sin B. cos C + cos B. sin C = 289/289 = 1

Evaluate the values of: (i) cos A  (ii) cosec A (iii) tan²A – sec²A  (iv) sin C (v) sec C  (vi) cot² C – 1/sin² C from the following diagram.

Solution:

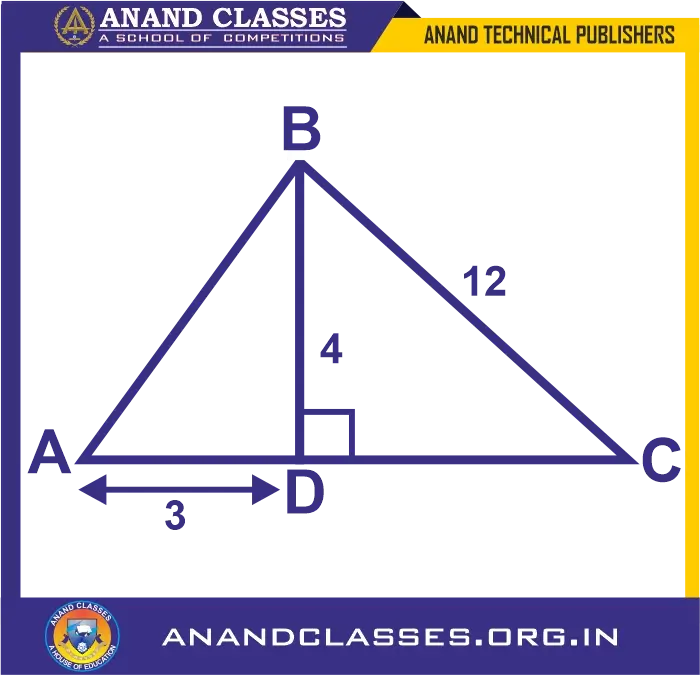
Considering the given diagram, we have

∠ADB = 90^o and ∠BDC = 90^o

So, by Pythagoras theorem

AB² = AD² + BD² (As AB is the hypotenuse in ∆ABD)

AB² = 3² + 4² = 9 + 16 = 25

Taking square root on both sides, we get

AB = 5

Also,

BC² = BD² + DC² (As BC is the hypotenuse in ∆BDC)

DC² = BC² – BD²

DC² = 12² – 4² = 144 – 16 = 128

Taking square root on both sides, we get

DC = 8√2

Now,

(i) cos A = base/hypotenuse

cos A = AD/AB

cos A = 3/5

(ii) cosec A = hypotenuse/perpendicular

cosec A = AB/BD

cosec A = 5/4

(iii) tan A = perpendicular/base

tan A = BD/AD

tan A = 4/3

sec A = hypotenuse/base

sec A = AB/AD

sec A = 5/3

tan² A – sec² A = (4/3)² – (5/3)²

tan² A – sec² A = 16/9 – 25/9

tan² A – sec² A = -9/9

tan² A – sec² A = -1

(iv) sin C = perpendicular/hypotenuse

sin C = BD/BC

sin C = 4/12

sin C = 1/3

(v) sec C = hypotenuse/base

sec C = BC/DC

sec C = 12/8√2

sec C = 3/2√2 = 3√2/4

(vi) cot C = base/perpendicular

cot C = DC/BD

cot C = 8√2/4

cot C = 2√2

sin C = perpendicular/hypotenuse

sin C = BD/BC

sin C = 4/12

sin C = 1/3

Now,

cot² C – 1/sin² C = (2√2)² – 1/(1/3)²

cot² C – 1/sin² C = 8 – 1/(1/9)

cot² C – 1/sin² C = 8 – 9

cot² C – 1/sin² C = -1

Evaluate the values of: (i) sin B  (ii) tan C (iii) sec² B – tan²B  (iv) sin²C + cos²C from the following diagram.

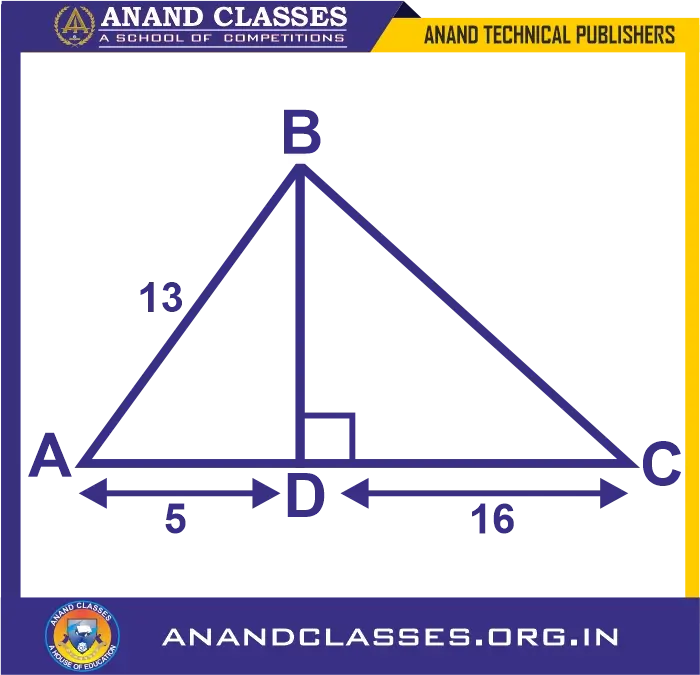
Solution:

From the figure, we have

∠ADB = 90^o and ∠ADC = 90^o

So, by Pythagoras theorem

AB² = AD² + BD² (As AB is the hypotenuse in ∆ABD)

13² = AD² + 5²

AD² = 13² – 5² = 169 – 25 = 144

Taking square root on both sides, we get

AD = 12

Also,

AC² = AD² + DC² (As AC is the hypotenuse in ∆ADC)

AC² = 12² + 16² = 144 + 256 = 400

Taking square root on both sides, we get

AC = 20

Now,

(i) sin B = perpendicular/hypotenuse = AD/AB = 12/13

(ii) tan C = perpendicular/base = 12/16 = 3/4

(iii) sec B = hypotenuse/base = AB/BD = 13/5

tan B = perpendicular/base = AD/BD = 12/5

Hence,

sec² B – tan² B = (13/5)² – (12/5)² = (169 – 144)/25 = 25/25 = 1

(iv) sin C = perpendicular/hypotenuse = AD/AC = 12/20 = 3/5

cos C = base/hypotenuse = DC/AC = 16/20 = 4/5

Hence,

sin² C + cos² C = (3/5)² + (4/5)² = (9 + 16)/25 = 25/25 = 1

Evaluate the values of: (i) sin A (ii) sec A (iii) cos² A + sin²A from the following diagram.

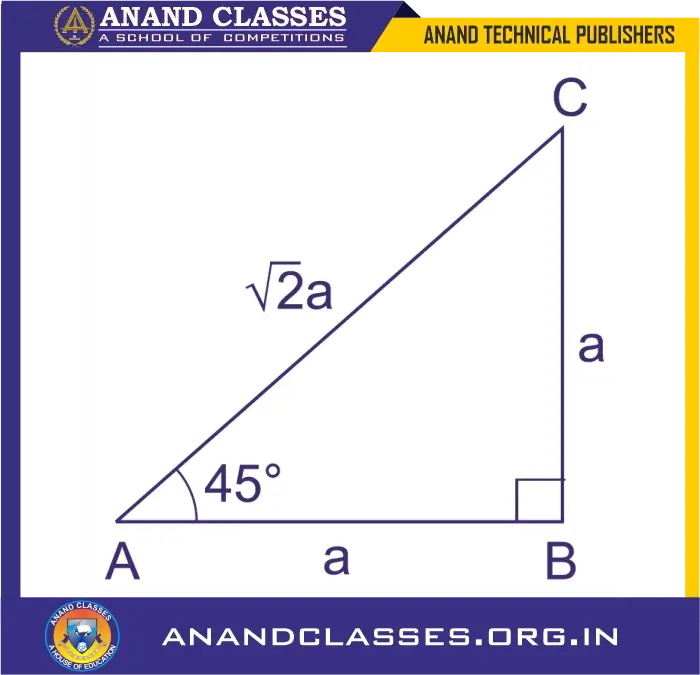
Solution:

From the given figure, we have

∠ABC = 90^o and AC is the hypotenuse ∆ABC

So, by Pythagoras Theorem

AC² = AB² + BC² = a² + a² = 2a²

Taking square root on both sides, we get

AC = √2a

Now,

(i) sin A = perpendicular/hypotenuse= BC/AB = a/√2a = 1/√2

(ii) sec A = hypotenuse/base = AC/AB = √2a/a = √2

(iii) sin A = perpendicular/hypotenuse = BC/AC = a/√2a = 1/√2

cos A = base/hypotenuse = AB/AC = a/√2a = 1/√2

Hence,

cos² A + sin² A = (1/√2)² + (1/√2)² = ½ + ½ = 1

From the following diagram, find: (i) Y (ii) sin x^o (iii) (sec x^o – tan x^o) (sec x^o + tan x^o)

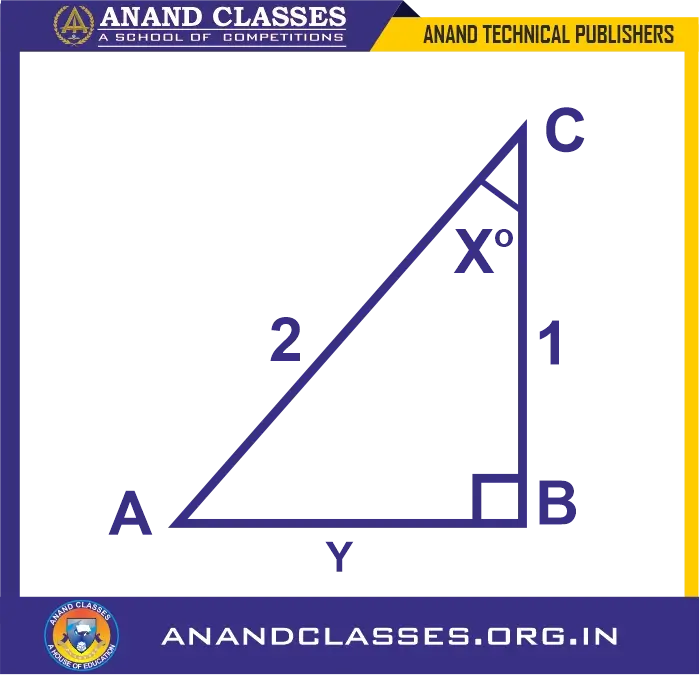
Solution:

From the given diagram,

(i) As it’s a right-angled triangle, so using Pythagorean Theorem

2² = y² + 1²

y² = 2² – 1²

y² = 4 – 1

y² = 3

Taking square root on both sides, we get

y = √3

(ii) sin x^o = perpendicular/hypotenuse = √3/2

(iii) tan x^o = perpendicular/base = √3

sec x^o = hypotenuse/base = 2

Therefore,

(sec x^o – tan x^o) (sec x^o + tan x^o) = (2 – √3)(2 + √3)

(sec x^o – tan x^o) (sec x^o + tan x^o) = 4 – √3 = 1

Evaluate (i) sin x^o  (ii) cos y^o (iii) 3 tan x^o – 2 sin y^o + 4 cos y^o from the following diagram

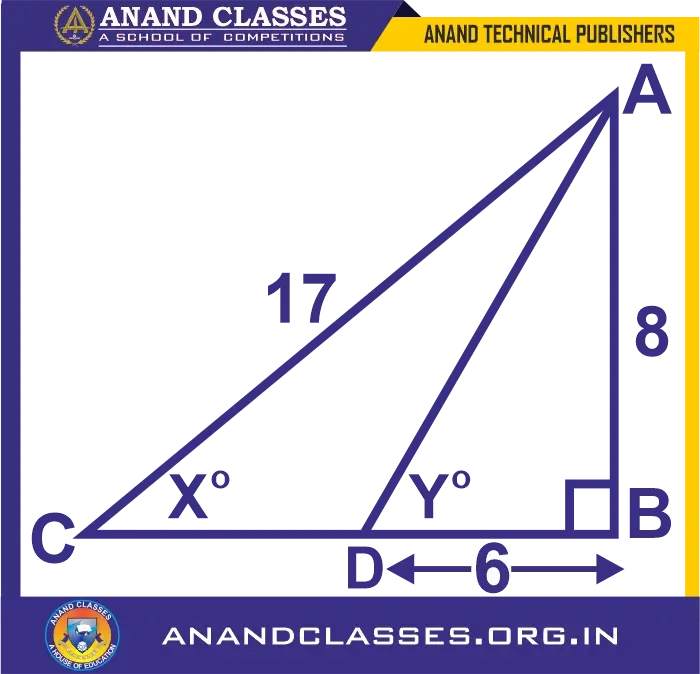
Solution:

Let’s consider the given figure,

As the triangle is a right-angled triangle, so using Pythagorean Theorem

AD² = 8² + 6² = 64 + 36 = 100

Taking square root on both sides, we get

AD = 10

Also, by Pythagorean Theorem

BC² = AC² – AB² = 17² – 8² = 289 – 64 = 225

Taking square root on both sides, we get

BC = 15

Now,

(i) sin x^o = perpendicular/hypotenuse = 8/17

(ii) cos y^o = base/hypotenuse = 6/10 = 3/5

(iii) sin y^o = perpendicular/base = AB/AD = 8/10 = 4/5

And,

cos y^o = 6/10 = 3/5

So,

tan x^o = perpendicular/base = AB/BC = 8/15

Therefore,

3 tan x^o – 2 sin y^o + 4 cos y^o =

= 3(8/15) – 2(4/5) + 4(3/5)

= 8/5 – 8/5 + 12/5 = 12/5

In the diagram, given below, triangle ABC is right-angled at B and BD is perpendicular to AC. Find: (i) cos ∠DBC (ii) cot ∠DBA

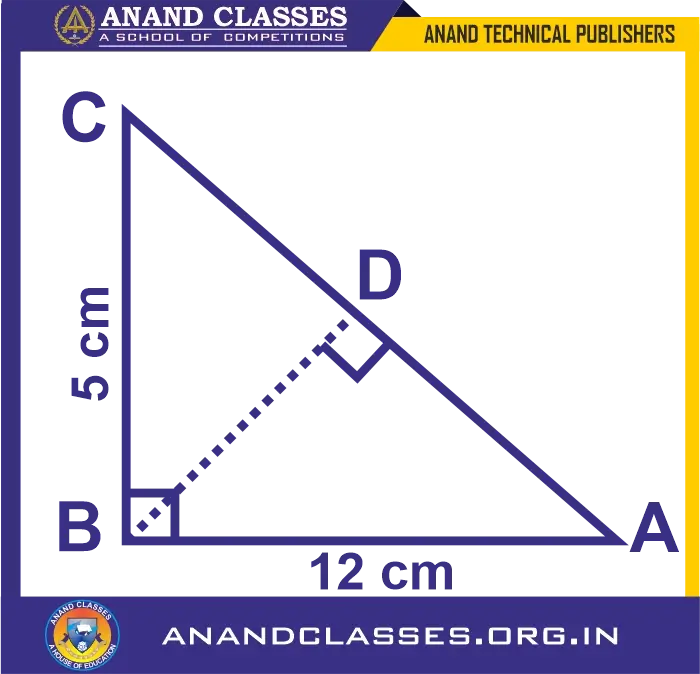
Solution:

Let’s consider the given figure,

As the triangle is a right-angled triangle, so using Pythagorean Theorem

AC² = 5² + 12² = 25 + 144 = 169

Taking square root on both sides, we get

AC = 13

In ∆CBD and ∆CBA,

∠C is common to both the triangles

∠CDB = ∠CBA = 90^o

Hence, ∠CBD = ∠CAB

Thus, ∆CBD and ∆CBA are similar triangles according to A criterion

So, we have

AC/BC = AB/BD

13/5 = 12/BD

BD = 60/13

Now,

(i) cos ∠DBC = base/hypotenuse = BD/BC = (60/13)/5 = 12/13

(ii) cot ∠DBA = base/perpendicular = BD/AB = (60/13)/12 = 5/13

In the given diagram, triangle ABC is right-angled at B. D is the foot of the perpendicular from B to AC. Given that BC = 3 cm and AB = 4 cm. Find: (i) tan ∠DBC (ii) sin ∠DBA

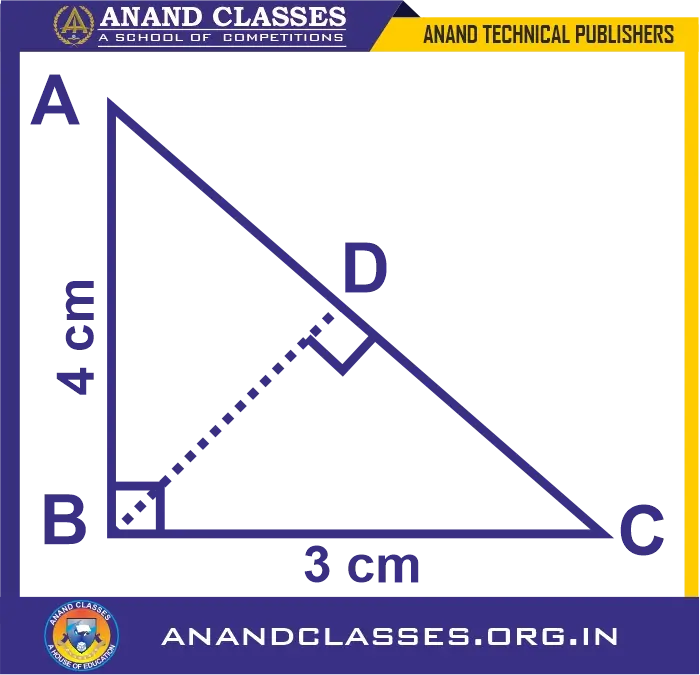
Solution:

Considering the given figure, we have

A right-angled triangle ABC, so by using Pythagorean Theorem we have

AC² = BC² + AB² = 4² + 3² = 16 + 9 = 25

Taking square root on both sides, we get

AC = 5

In ∆CBD and ∆CAB, we have

∠BCD = ∠ACB (Common)

∠CDB = ∠CBA = 90^o

Hence, ∆CBD ~ ∆CAB by A similarity criterion

So,

AC/BC = AB/BD

5/3 = 4/BD

BD = 12/5

Now, using Pythagorean Theorem in ∆BDC

DC² = BC² – BD²

DC² = 3² – (12/5)² = 9 – 144/25 = (225 – 144)/25

= 81/25

Taking square root on both sides, we get

DC = 9/5

Therefore,

AD = AC – DC = 5 – 9/5 = 16/5

Now,

(i) tan ∠DBC = perpendicular/ base = DC/BD = (9/5)/(12/5) = 3/4

(ii) sin ∠DBA = AD/AB = (16/5)/4 = 4/5

From the following diagram, In triangle ABC, AB = AC = 15 cm and BC = 18 cm, find cos ∠ABC.

Solution:

Let’s consider the diagram below:

 In the isosceles ∆ABC, we have

AB = AC = 15 cm

BC = 18 cm

Now, the perpendicular drawn from angle A to its opposite BC divides its into two equal parts

i.e., BD = DC = 9cm

Hence,

cos ∠ABC = base/hypotenuse

cos ∠ABC = BD/AB = 9/15 = 3/5

In the diagram given below, ABC is an isosceles triangle with BC = 8 cm and AB = AC = 5 cm. Find: (i) sin B  (ii) tan C (iii) sin² B + cos²B  (iv) tan C – cot B

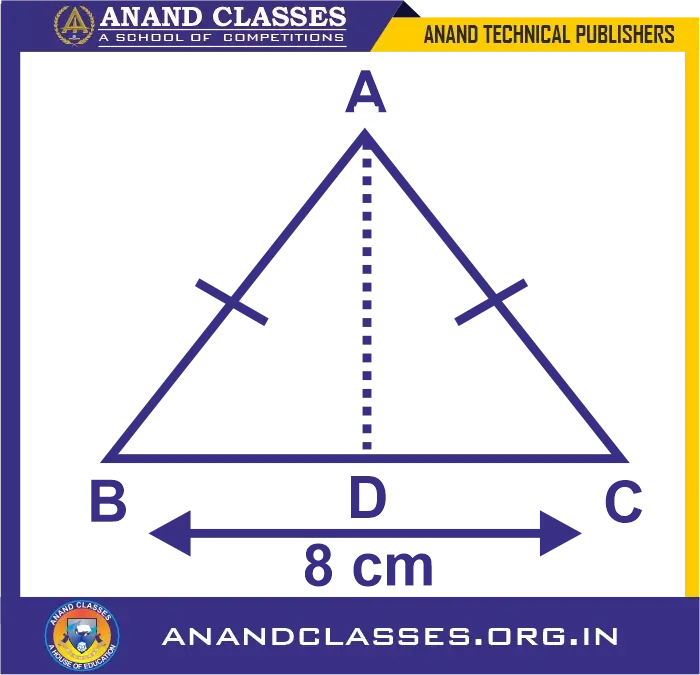
Solution:

In the isosceles ∆ABC, we have

AB = AC = 5 cm

BC = 8 cm

Now, the perpendicular drawn from angle A to its opposite BC divides its into two equal parts

i.e., BD = DC = 4cm

As, ∠ADB = 90^o in ∆ABD, we have

AB² = AD² + BD²

AD² = AB² – BD²

AD² = 5² – 4² = 25 – 16 = 9

Taking square root on both sides, we get

AD = 3

Now,

(i) sin B = AD/AB = 3/5

(ii) tan C = AD/DC = 3/4

(iii) sin B = AD/AB

= 3/5

cos B = BD/AB = 4/5

Hence,

sin² B + cos² B = (3/5)² + (4/5)²

sin² B + cos² B = 9/25 + 16/25 = 25/25 = 1

(iv) tan C = AD/DC = 3/4

cot B = BD/AD = 4/3

Hence,

tan C – cot B = 3/4 – 4/3 = (9 – 16)/12 = -7/12

In triangle ABC; ∠ABC = 90^o, ∠CAB = x^o, tan x^o = 3/4 and BC = 15 cm. Find the measures of AB and AC.

Solution:

Let’s consider the figure below:

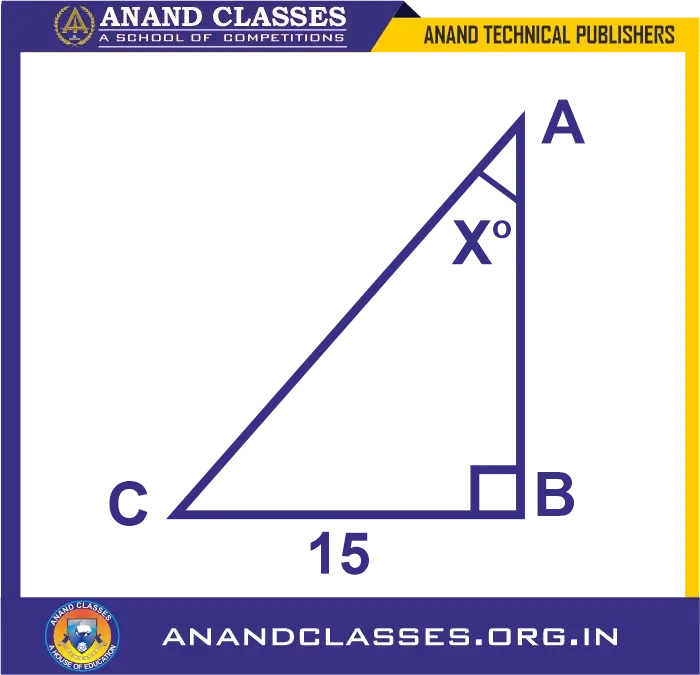
Given, tan x^o = 3/4

tan x^o = perpendicular/base = 3/4

BC/AB = 3/4

Hence,

If length of base AB = 4x, the length of perpendicular BC = 3x

So, by Pythagoras Theorem

BC² + AB² = AC²

(3x)² + (4x)² = AC²

AC² = 9x² + 16x² = 25x²

Taking square root on both sides, we get

AC = 5x, which is the hypotenuse

Now, we have

BC = 15

⇒ 3x = 15

x = 5

Therefore, AB = 4x = 4(5) = 20 cm

And, AC = 5x = 5 × 5 = 25 cm

Using the measurements given in the following diagram : (i) Find the value of sin Ø and tan θ (ii) Write an expression for AD in terms of θ

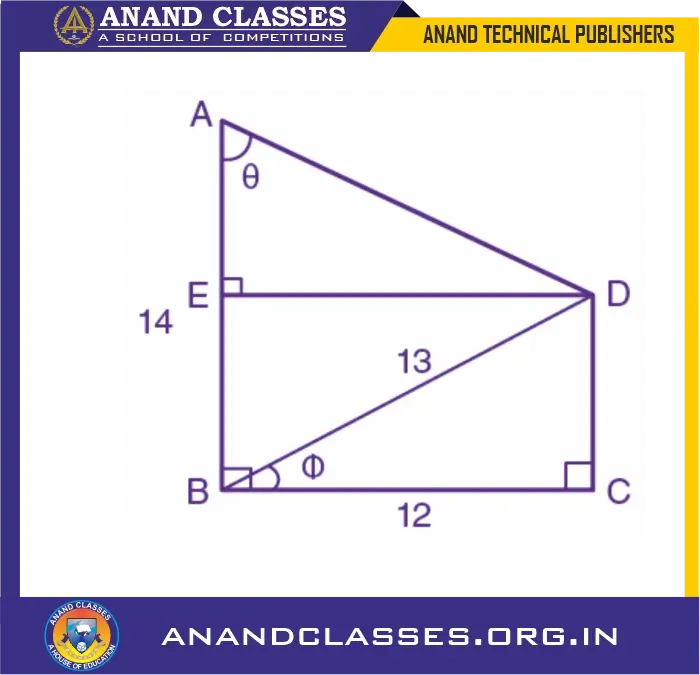
Solution:

Let’s consider the figure above:

Constructing a perpendicular from D to the side AB at point E which makes BCDE a rectangle.

Now, in right angled ∆BCD using Pythagorean Theorem, we have

BD² = BC² + CD² [As AB is the hypotenuse]

CD² = BD² – BC²

CD² = 13² – 12²

CD² = 169 – 144 = 25

Taking square root on both sides, we get

CD = 5

As BCDE is a rectangle,

ED = 12 cm, EB = 5 cm and AE = (14 – 5) cm = 9 cm

Now,

(i) sin Ø = CD/BD = 5/13

tan θ = ED/AE = 12/9 = 4/3

(ii) sec θ = AD/AE = AD/9

AD = 9 sec θ

Or

cosec θ = AD/ED

cosec θ = AD/12

AD = 12cosec θ

In the given diagram : BC = 15 cm and sin B = 4/5.(i) Calculate the measure of AB and AC. (ii) Now, if tan ∠ADC = 1; calculate the measures of CD and AD. Also, show that: tan²B – 1/cos² B = -1

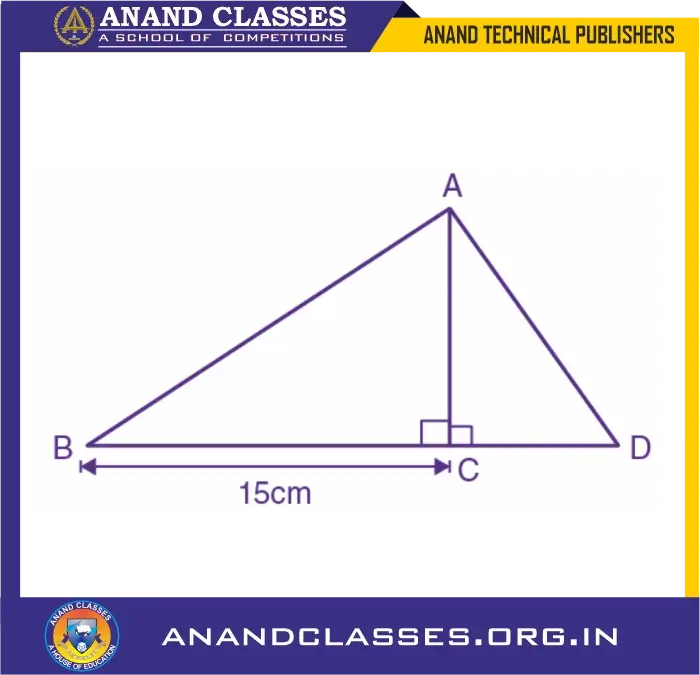
Solution:

Given, BC = 15 cm and sin B = 4/5

⇒ Perpendicular/hypotenuse = AC/AB

sin B = 4/5 = AC/AB

Hence, if the length of perpendicular is AC = 4x, the length of hypotenuse will be AB = 5x

In right triangle ABC, we have

BC² + AC² = AB² [By Pythagoras Theorem]

BC² = AB² – AC²

BC² = (5x)² – (4x)²

BC² = 25x² – 16x²

BC² = 9x²

Taking square root on both sides, we get

BC = 3x

Now, as BC = 15 (given)

3x = 15

x = 15/3

x = 5

(i) AC = 4x = 4(5) = 20 cm

And,

AB = 5x = 5(5) = 25 cm

(ii) Given,

tan ∠ADC = 1

perpendicular/base = AC/CD = 1/1

Hence, If length of perpendicular is x, then the length of hypotenuse will be x

And, we have

AC² + CD² = AD² [Using Pythagoras Theorem]

x² + x² = AD²

AD² = 2x²

Taking square root on both sides, we get

AD = √2x

Now,

AC = 20 ⇒x = 20

So,

AD = √2x = √2(20) = 20√2 cm

And,

CD = 20 cm

Hence,

tan B = AC/BC = 20/15 = 4/3

cos B = BC/AB = 15/25 = 3/5

Thus,

tan² B – 1/cos² B = (4/3)² – 1/(3/5)²

tan² B – 1/cos² B = 16/9 – 1/(9/25)

tan² B – 1/cos² B = 16/9 – 25/9 = – 9/9 = -1