ANAND CLASSES Study Material and Notes to Strengthen your Class 10 Mathematics with essential solved examples on Trigonometric Ratios for NTSE JEE Foundation. Learn step-by-step problem-solving techniques to score higher in exams.
[related_inline_dropdown]
Express the trigonometric ratios cos A, tan A and sec A in terms of sin A.
Solution:
We know that,
sin2 A + cos2 A = 1
So,
cos A = √(1 – sin2 A)
tan A = sin A/cos A = sin A/ √(1 – sin2 A)
sec A = 1/cos A = 1/ (√1 – sin2 A)
Follow the Figure for the following problems
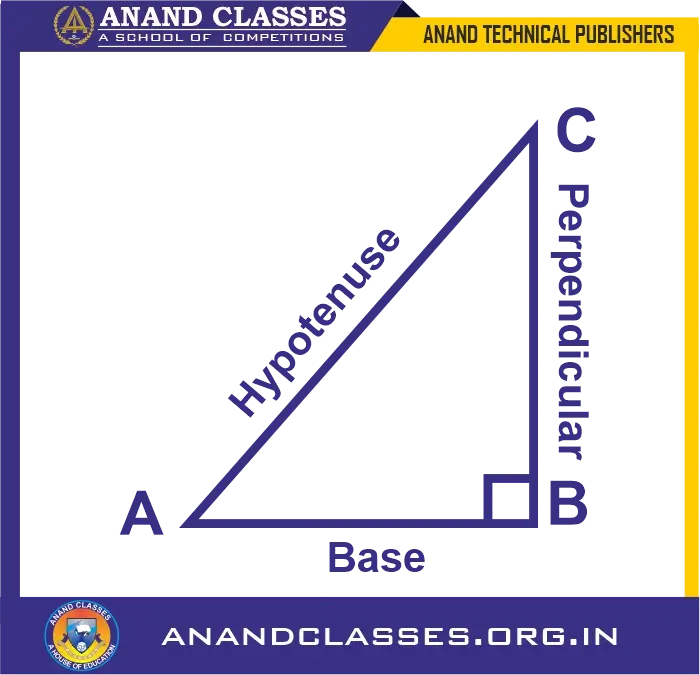
If A is an acute angle and sin A = 3/5, find all other trigonometric ratios of angle A (using trigonometric identities).
Solution:
Given, sin A = 3/5 and A is an acute angle
So, in ∆ABC we have ∠B = 90o
And, AC = 5 and BC = 3
By Pythagoras theorem,
AB = √(AC2 – BC2)
AB = √(52 – 32) = √(25 – 9) = √16 = 4
Now,
cos A = AB/AC = 4/5
tan A = BC/AB = 3/4
cot A = 1/tan θ = 4/3
sec A = 1/cos θ = 5/4
cosec A = 1/sin θ = 5/3
If A is an acute angle and sec A = 17/8, find all other trigonometric ratios of angle A (using trigonometric identities).
Solution:
Given, sec A = 17/8 and A is an acute angle
So, in ∆ ABC we have ∠B = 90o
And, AC = 17 and AB = 8
By Pythagoras theorem,
BC = √(AC2 – AB2)
BC = √(172 – 82) = √(289 – 64) = √225 = 15
Now,
sin A = BC/AC = 15/17
cos A = 1/sec A = 8/17
tan A = BC/AB = 15/8
cot A = 1/tan A= 8/15
cosec A = 1/sin A = 17/15
If tan A = 1/√3, find all other trigonometric ratios of angle A.
Solution:
Given, tan A = 1/√3
In the right ∆ ABC, we have ∠B = 90o
tan A = BC/AB = 1/√3
So,
BC = 1 and AB = √3
By Pythagoras theorem,
AC = √(AB2 + BC2) = √[(√3)2 + (1)2]
AC = √(3 + 1) = √4 = 2
Hence,
sin A = BC/AC = ½
cos A = AB/AC = √3/2
cot A = 1/tan A = √3
sec A = 1/cos A = 2/√3
cosec A = 1/sin A = 2/1 = 2
If 12 cosec θ = 13, find the value of (2 sin θ – 3 cos θ)/ (4 sin θ – 9 cos θ)
Solution:
Given,
12 cosec θ = 13
⇒ cosec θ = 13/12
In right ∆ ABC, we have ∠B = 90o
∠A = θ
So, cosec θ = AC/BC = 13/12
AC = 13 and BC = 12
By Pythagoras theorem,
AB = √(AC2 – BC2)
AB = √[(13)2 – (12)2]
AB = √(169 – 144)
AB = √25 = 5
Now,
sin θ = BC/AC = 12/13
cos θ = AB/AC = 5/13
Hence,
(2 sin θ – 3 cos θ)/ (4 sin θ – 9 cos θ)
= (2 x 12/13 – 3 x 5/13)/(4 x 12/13 – 9 x 5/13) = 3
Given: sin A = 3/5, find: (i) tan A (ii) cos A
Solution:
In right ∆ ABC, we have ∠B = 90o
Given, sin A = 3/5
⇒ perpendicular/hypotenuse = 3/5
BC/AC = 3/5
Hence,
If the length of BC is 3x, the length of AC is 5x
We have,
AB2 + BC2 = AC2 [By Pythagoras Theorem]
AB2 + (3x)2 = (5x)2
AB2 = 25x2 – 9x2
= 16x2
Taking square root on both sides, we get
AB = 4x, which is the base
Now,
(i) tan A = perpendicular/base
= 3x/4x
= 3/4
(ii) cos A = base/hypotenuse
= 4x/5x
= 4/5
Given: cos A = 5/13 Evaluate: (i) (sin A – cot A)/2tan A (ii) cot A + 1/cos A
Solution:
In right ∆ ABC, we have ∠B = 90o
Given, cos A = 5/13
⇒ base/hypotenuse = 5/13
AB/AC = 5/13
Hence,
If length of AB = 5x, the length of AC = 13x
So, by Pythagoras Theorem
AB2 + BC2 = AC2
(5x)2 + BC2 = (13x)2
BC2 = 169x2 – 25x2
= 144x2
Taking square root on both sides, we get
BC = 12x, which is the perpendicular
Now,
tan A = perpendicular/base
= 12x/5x
= 12/5
sin A = perpendicular/base
= 12x/13x
= 12/13
cot A = base/perpendicular
= 5x/12x
= 5/12
(i) (sin A – cot A)/2tan A = [(12/13) – (5/12)]/ 2(12/5)
= 79/156 x 5/24
= 395/3744
(ii) cot A + 1/cos A = 5/12 + 1/(5/13)
= 5/12 + 13/5
= 181/60
Given: sec A = 29/21, evaluate: sin A – 1/tan A
Solution:
In right ∆ ABC, we have ∠B = 90o
Given, sec A = 29/21
⇒ hypotenuse/base = 29/21
AC/AB = 29/21
Hence,
If length of AB = 21x, the length of AC = 29x
So, by Pythagoras Theorem
AB2 + BC2 = AC2
(21x)2 + BC2 = (29x)2
BC2 = 841x2 – 441x2
= 400x2
Taking square root on both sides, we get
BC = 20x, which is the perpendicular
Now,
sin A = perpendicular/hypotenuse
= 20x/29x
= 20/29
tan A = perpendicular/base
= 20x/21x
= 20/21
Therefore,
sin A – 1/tan A = 20/29 – 1/(20/21)
= 20/29 – 21/20
= – 209/580
Given: tan A = 4/3, find: cosec A/(cot A – sec A)
Solution:
In right ∆ ABC, we have ∠B = 90o
Given, tan A = 4/3
⇒ perpendicular/base = 4/3
BC/AB = 4/3
Hence,
If length of AB = 3x, the length of BC = 4x
So, by Pythagoras Theorem
AB2 + BC2 = AC2
(3x)2 + (4x)2 = AC2
AC2 = 9x2 + 16x2
= 25x2
Taking square root on both sides, we get
AC = 5x, which is the hypotenuse
Now,
sec A = hypotenuse/base
= AC/AB
= 5x/3x
= 5/3
cot A = base/perpendicular
= AB/BC
= 3x/4x
= ¾
cosec A = hypotenuse/perpendicular
= AC/BC
= 5x/4x
= 5/x
Therefore,
cosec A/(cot A – sec A) = (5/4)/(3/4 – 5/3)
= (5/4)/(-11/12)
= – 60/44
= – 15/11
Given: 4 cot A = 3, find; (i) sin A (ii) sec A (iii) cosec2 A – cot2A.
Solution:
In right ∆ ABC, we have ∠B = 90o
Given, 4 cot A = 3
cot A = 3/4
⇒ base/perpendicular = 4/3
AB/BC = 3/4
Hence,
If length of AB = 3x, the length of BC = 4x
So, by Pythagoras Theorem
AB2 + BC2 = AC2
(3x)2 + (4x)2 = AC2
AC2 = 9x2 + 16x2
= 25x2
Taking square root on both sides, we get
AC = 5x, which is the hypotenuse
Now,
(i) sin A = perpendicular/hypotenuse
= 4x/5x
= 4/5
(ii) sec A = hypotenuse/base
= AC/AB
= 5x/3x
= 5/3
(iii) cosec A = hypotenuse/perpendicular
= AC/BC
= 5x/4x
= 5/4
cot A = 3/4
Hence,
cosec2 A – cot2 A = (5/4)2 – (3/4)2
= (25 – 9)/16
= 16/16
= 1
Find Sin A and Sec A, if 15 cot A = 8.
Solution:
Given that 15 cot A = 8
Therefore, cot A = 8/15.
We know that tan A = 1/ cot A
Hence, tan A = 1/(8/15) = 15/8.
Thus, Side opposite to ∠A/Side Adjacent to ∠A = 15/8
Let BC be the side opposite to ∠A and AB be the side adjacent to ∠A and AC be the hypotenuse of the right triangle ABC, respectively.
Hence, BC = 15x and AB = 8x.
Hence, to find the hypotenuse side, we have to use the Pythagoras theorem.
(i.e) AC2 = AB2 + BC2
AC2 = (8x)2+(15x)2
AC2 = 64x2+225x2
AC2 = 289x2
AC = 17x.
Therefore, the hypotenuse AC = 17x.
Finding Sin A:
We know Sin A = Side Opposite to ∠A / Hypotenuse
Sin A = 15x/17x
Sin A = 15/17.
Finding Sec A:
To find Sec A, find cos A first.
Thus, cos A = Side adjacent to ∠A / Hypotenuse
Cos A = 8x/17x
We know that sec A = 1/cos A.
So, Sec A = 1/(8x/17x)
Sec A = 17x/8x
Sec A = 17/8.
Therefore, Sin A = 15/17 and sec A = 17/8.
If tan (A+ B) =√3, tan (A-B) = 1/√3, then find A and B. [Given that 0° <A+B ≤ 90°; A>B ]
Solution:
Given that
Tan (A+B) = √3.
We know that tan 60 = √3.
Thus, tan (A+B) = tan 60° = √3.
Hence A+B= 60° …(1)
Similarly, given that,
Tan (A-B) = 1/√3.
We know that tan 30° = 1/√3.
Thus, tan (A-B) = tan 30° = 1/√3.
Hence, A-B = 30° …(2)
Now, adding the equations (1) and (2), we get
A+B+A-B = 60° + 30°
2A = 90°
A = 45°.
Now, substitute A = 45° in equation (1), we get
45° +B = 60°
B = 60°- 45°
B = 15°
Hence, A = 45 and B = 15°.
💡 Do You Know?
- The values of trigonometric ratios are exact for 0°, 30°, 45°, 60°, and 90°.
- These ratios are frequently used in geometry, physics, astronomy, and engineering.
- The identities like sin²θ + cos²θ = 1 help derive all other formulas in trigonometry.
📘 Quick Summary Table
| Angle | sin | cos | tan | sec | cosec | cot |
|---|---|---|---|---|---|---|
| 0° | 0 | 1 | 0 | 1 | – | – |
| 30° | 1/2 | √3/2 | 1/√3 | 2/√3 | 2 | √3 |
| 45° | 1/√2 | 1/√2 | 1 | √2 | √2 | 1 |
| 60° | √3/2 | 1/2 | √3 | 2 | 2/√3 | 1/√3 |
| 90° | 1 | 0 | – | – | 1 | 0 |
Trigonmetric Identities Table Summary
| Identities Name | Identities |
|---|---|
| Pythagorean Identities | sin2θ + cos2θ = 1 |
| 1 + tan2θ = sec2θ | |
| 1 + cot2θ = cosec2θ | |
| Reciprocal Identities | cosec θ = 1/sin θ |
| sec θ = 1/cos θ | |
| cot θ = 1/tan θ | |
| Quotient Identities | tan θ = sin θ/cos θ |
| cot θ = cos θ/sin θ |









