Speed(Velocity)-Time Graphs Cases, Area Under Speed-Time Curve Gives Distance Travel

ANAND CLASSES study material and notes to learn Speed-Time Graphs in detail with mathematical derivations, proofs, exam-based questions, MCQs, and worksheets. Ideal for JEE, NEET, and CBSE Class 11 students.

Types of Speed-Time Graphs with Detailed Explanation and Proofs

1. Speed-Time Graph When Speed Remains Constant

• When the speed of a body remains constant, there is no acceleration.
• The speed-time graph is a straight horizontal line parallel to the time axis.
• The area under the graph gives the distance traveled.

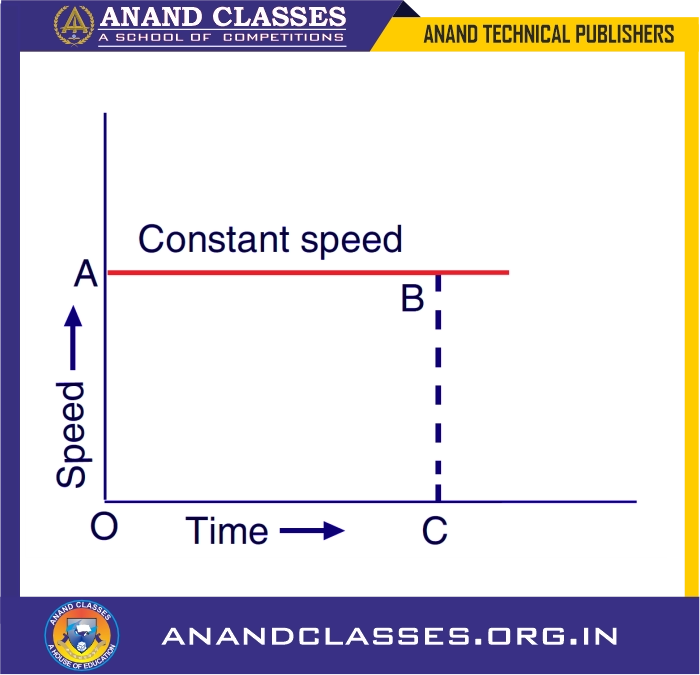
Mathematical Derivation:

Since the speed remains constant, we use the formula: $$\text{Speed} = \frac{\text{Distance}}{\text{Time}}$$

Rearranging for distance: $$\text{Distance} = \text{Speed} \times \text{Time}$$

From the graph, this corresponds to the area of the rectangle formed under the speed-time curve:

$$\text{Distance} = \text{OA} \times \text{OC}$$

Thus, the total distance traveled by the body is equal to the area under the speed-time graph.

2. Speed-Time Graph When Speed Changes at a Uniform Rate (Uniform Acceleration)

• The speed-time graph is a straight line with a positive slope.
• Acceleration is given by the slope of the graph.
• The distance traveled is given by the area under the graph, which forms a triangle.

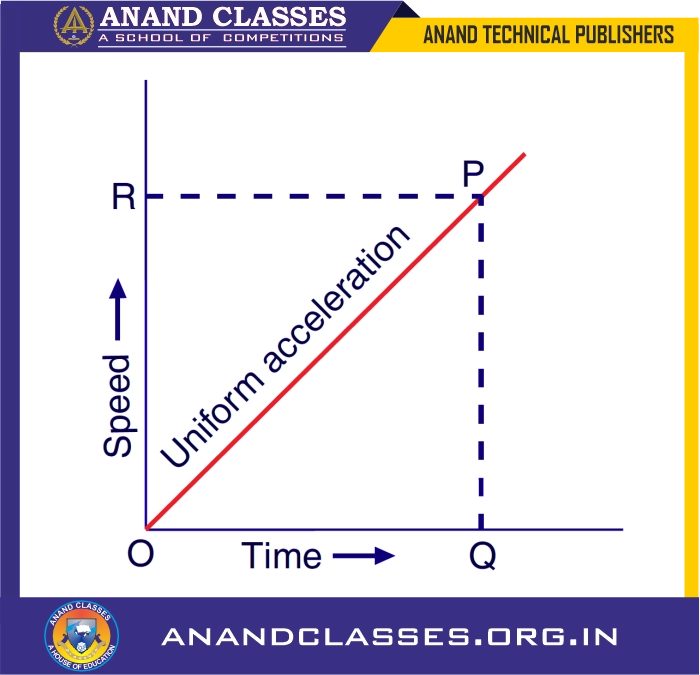
Mathematical Derivation:

We define acceleration as: $$ a = \frac{v – u}{t}$$

where:

• $u$ = initial speed
• $v$ = final speed
• $t$ = time

The change in speed is represented by PQ whereas time taken is equal to OQ. So,

$$ a = \frac{PQ}{OQ}$$

But $ \frac{PQ}{OQ}$ is the slope (or gradient) of the speed-time graph OP, therefore, we conclude that in a speed-time graph, the acceleration is given by the slope of the graph. In other words, the slope of a speed-time graph of a moving body gives its acceleration.

From the speed-time graph, the distance traveled is given by the area under the curve OPQ.

The distance travelled by the body in the time corresponding to point Q will be equal to the area of the triangle OPQ, which is equal to half the area of the rectangle ORPQ.
Thus, Distance travelled = Area of triangle OPQ

$$\text{Distance} = \frac{1}{2}\times\text{OR} \times \text{OQ}$$

Thus, the total distance traveled by the body is equal to the area under the speed-time graph.

3. Speed-Time Graph When the Initial Speed of a body is not zero

In this case speed-time graph when the initial speed of a body is not zero and to determine the distance traveled using the area under the graph.

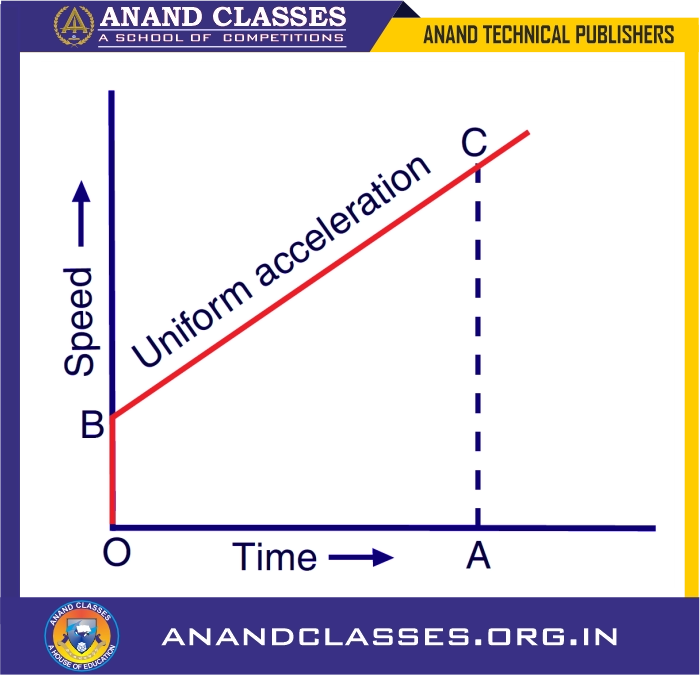
1. Graph Explanation:
   • The speed-time graph represents an object that starts with an initial speed OB and accelerates uniformly to speed AC over time OA.
   • The curve is a straight line (uniform acceleration).
2. Acceleration Calculation:
   • The acceleration aa can be determined using: $$a = \frac{\text{final speed} – \text{initial speed}}{\text{time}} $$ $$a = \frac{AC – OB}{OA}$$
3. Distance Calculation Using Area Under Graph:
   • The area under the speed-time graph represents the distance traveled.
   • The shape OBCA is a trapezium.
   • The area of a trapezium is given by: $$\text{Area} = \frac{\text{sum of parallel sides} \times \text{height}}{2}$$
   • In this case:
     • Parallel sides: OB and AC
     • Height: OA
     • So, distance traveled is: $$\text{Distance} =\frac{(OB + AC) \times OA}{2}$$

4. Speed-Time Graph When Speed Changes at a Non-Uniform Rate (Non-Uniform Acceleration)

• The graph is a curve indicating varying acceleration.
• Distance traveled is given by the area under the curve.

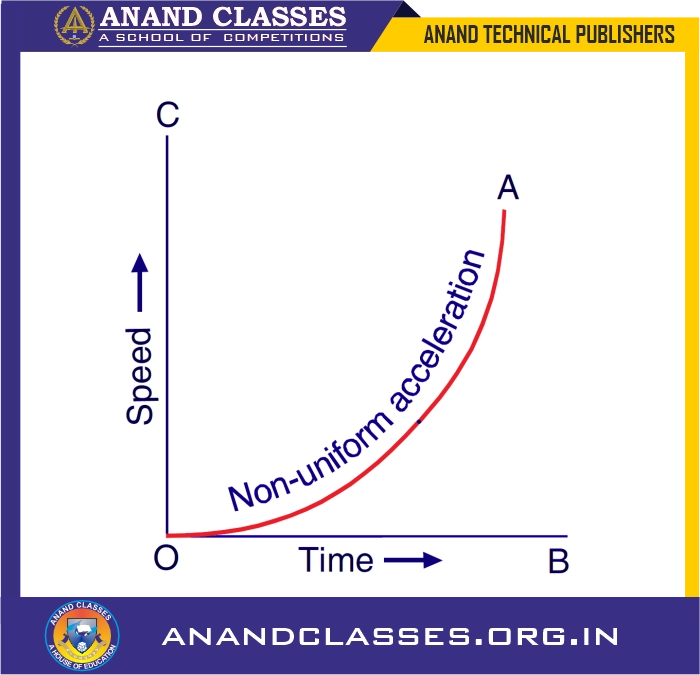
Mathematical Interpretation:

Since acceleration is not constant, we need to integrate the velocity function: $$s = \int v(t)\; dt$$

If the velocity function$\;v(t)$ is known, we can integrate it to find the total distance traveled.

Question-Answer Format for Exams (JEE, NEET, CBSE Class 11)

Q1: What does the slope of a speed-time graph represent?

A: The slope represents acceleration. A positive slope indicates acceleration, while a negative slope indicates deceleration.

Q2: How can distance traveled be determined from a speed-time graph?

A: Distance traveled is given by the area enclosed between the speed-time curve and the time axis.

Q3: What does a horizontal line on a speed-time graph indicate?

A: It indicates uniform speed, meaning there is no acceleration.

MCQs with Answers and Explanations

Q1: The speed-time graph of a body moving with uniform velocity is:

• (A) A straight line parallel to the time axis
• (B) A straight line passing through the origin
• (C) A curve
• (D) A straight line with a negative slope
  Answer: (A) A straight line parallel to the time axis
  Explanation: A uniform speed means no acceleration, so the graph remains constant over time.

Q2: The acceleration of an object is found using which part of the speed-time graph?

• (A) The area under the graph
• (B) The slope of the graph
• (C) The intercept on the speed axis
• (D) None of these
  Answer: (B) The slope of the graph
  Explanation: Acceleration is the rate of change of speed with respect to time, which is represented by the slope.

Do You Know?

• A curved speed-time graph means the acceleration is changing.
• The area under a velocity-time graph gives displacement, whereas the area under a speed-time graph gives distance.
• If acceleration is negative, the object is decelerating.

Worksheet

1. Draw a speed-time graph for an object moving with constant acceleration.
2. How do you determine acceleration from a speed-time graph?
3. A car moves with an initial speed of 5 m/s and accelerates uniformly to 20 m/s in 5 seconds. Draw its speed-time graph and find the acceleration.

Test Paper (Marks Distribution)

Total Marks: 20

1. Define a speed-time graph and list its types. (4 Marks)
2. Explain the concept of acceleration using a speed-time graph. (4 Marks)
3. A car starts from rest and attains a velocity of 25 m/s in 5 seconds. Plot a speed-time graph and calculate the distance traveled. (6 Marks)
4. Multiple choice questions (2 questions) (6 Marks)

Important Points for Quick Revision

• Speed-time graphs represent motion and acceleration of a body.
• The slope of a speed-time graph gives acceleration.
• The area under the speed-time graph gives distance traveled.
• A straight-line speed-time graph represents uniform acceleration.
• A curved speed-time graph represents non-uniform acceleration.

Best Coaching Center for IIT-JEE, NEET, and Foundations

ANAND CLASSES

Buy complete study material at ANAND CLASSES Store
Proprietor: NIRMAL ANAND Educations
Written by: Neeraj Anand
Published by: Anand Technical Publishers
Contact: +91-9463138669
Email: anandclasses1996@gmail.com