ANAND CLASSES Study Material and Notes to learn Series and Parallel Combination of Resistances with Class 10 Science notes, formulas, MCQs, Assertion-Reason questions, worksheets, and test papers.
🔌 Combination of Resistances (or Resistors)
✅ Importance:
- Apart from potential difference, the current in a circuit also depends on the resistance of the circuit.
- In electrical circuits of radios, televisions, and other similar devices, it is usually necessary to combine two or more resistances to get the required current.
✅ Methods of Combining Resistors:
Resistances can be combined in two main ways:
- In Series
- In Parallel
📈 To Achieve Desired Resistance:
- To increase total resistance → Connect resistances in series
- To decrease total resistance → Connect resistances in parallel
Series Combination
🔹 Definition:
When two (or more) resistances are connected end to end consecutively, they are said to be connected in series.
🔹 Example:
- In Figure, two resistances $R_1$ and $R_2$ are connected in series.

Parallel Combination
🔹 Definition:
When two (or more) resistances are connected between the same two points, they are said to be connected in parallel.
🔹 Explanation:
- The resistors become parallel to one another in the arrangement.
🔹 Example:
- In Figure, the two resistances $R_1$ and $R_2$ are connected in parallel between the same two points A and B.

📌 Note:
- The examples above show only two resistances in each combination.
- However, any number of resistors can be connected in series or parallel arrangements.
🔗 Resistances (or Resistors) in Series
🔍 What is Series Combination of Resistors?
When multiple resistors are connected end to end, they form a series combination. The combined or resultant resistance of such a series connection is calculated using the law of combination of resistances in series.
📘 Law of Combination of Resistances in Series:
The total resistance of resistors connected in series is equal to the sum of their individual resistances.
📌 Formula:
If resistors $R_1, R_2, R_3, \ldots$ are connected in series, then the total or equivalent resistance R is: $$R = R_1 + R_2 + R_3 + \ldots$$
Note : Resultant resistance (R) is always greater than the largest individual resistance in the series group.
🔢 Example:
Let:
- $R_1 = 2 \, \Omega$
- $R_2 = 4 \, \Omega$
Then, $R = R_1 + R_2 = 2 + 4 = 6 \, \Omega$
✅ So, the combined resistance is 6 ohms.
📌 Important Points to Remember:
- When resistors in series are connected to a battery:
- Each resistor has a different potential difference across it, depending on its resistance.
- The total potential difference is equal to the voltage of the battery.
- So, $V = V_1 + V_2 + V_3 + \ldots$
- The same current flows through each resistor in a series combination.
- Note : Resultant resistance (R) is always greater than the largest individual resistance in the series group.
🧮 Derivation of Resultant Resistance of Two Resistors in Series
🔍 Setup:
- Two resistors: $R_1$ and $R_2$
- Applied voltage: V
- Current through the circuit: I
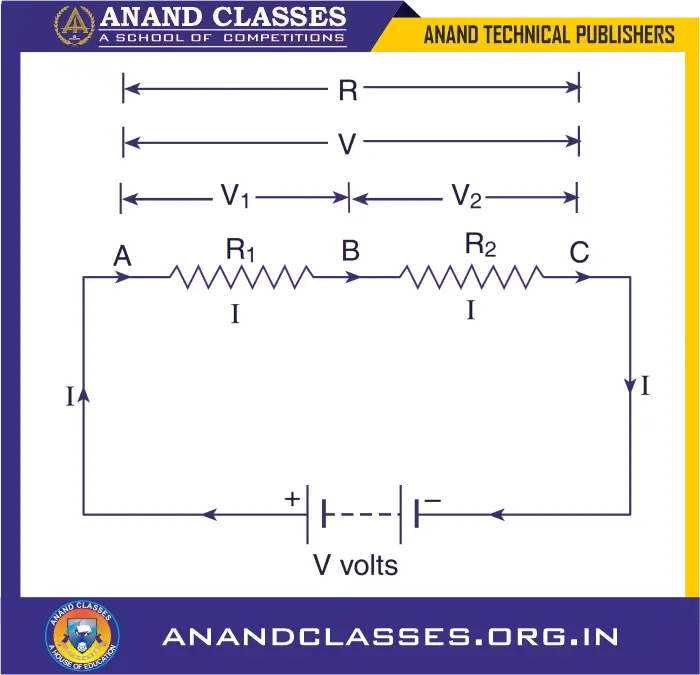
🔢 Step-by-step Derivation:
Total potential difference: $$V = V_1 + V_2 \tag{1}$$
From Ohm’s Law: $$V = I \times R \tag{2}$$ $$V_1 = I \times R_1 \tag{3} $$ $$V_2 = I \times R_2 \tag{4}$$
Substituting equations (2), (3), and (4) into (1): $$I \times R = I \times R_1 + I \times R_2$$
Canceling II from both sides: $$R = R_1 + R_2$$
✅ So, the resultant resistance for two resistors in series is: $$R = R_1 + R_2$$
Note : Resultant resistance (R) is always greater than the largest individual resistance in the series group.
🧮 Resultant Resistance of Three Resistors in Series
🔍 Setup:
- Resistors: $R_1, R_2, R_3$
- Applied voltage: V
- Current through circuit: I

🔢 Step-by-step Derivation:
Total potential difference: $$V = V_1 + V_2 + V_3 \tag{1}$$
From Ohm’s Law: $$V = I \times R \tag{2}$$ $$V_1 = I \times R_1 \tag{3}$$ $$V_2 = I \times R_2 \tag{4}$$ $$V_3 = I \times R_3 \tag{5}$$
Substituting values from (2)–(5) into (1): $$I \times R = I \times R_1 + I \times R_2 + I \times R_3$$
Canceling I: $$R = R_1 + R_2 + R_3$$
✅ So, the resultant resistance for three resistors in series is: $$R = R_1 + R_2 + R_3$$
Note : Resultant resistance (R) is always greater than the largest individual resistance in the series group.
🔄 Extension:
If four or more resistors are connected in series, then the total resistance is: $$R = R_1 + R_2 + R_3 + R_4 + \ldots$$
Sample Problems
Q: If four resistors of 1 Ω each are connected in series, what is the total resistance?
➤ Solution:
$$R = R_1 + R_2 + R_3 + R_4 = 1 + 1 + 1 + 1 = 4\, \Omega$$
Q: A 6 Ω and a 4 Ω resistor are connected in series. If a 20 V battery is applied across them, find (i) The current in the circuit (ii) The voltage across the 6 Ω resistor (iii) The voltage across the 4 Ω resistor
➤ Solution:
- Total Resistance, R = 6 + 4 = 10 Ω
- Voltage, V = 20 V

$$I = \frac{V}{R} = \frac{20}{10} = 2\, \text{A}$$
Voltage across 6 Ω: $$V = I \times R = 2 \times 6 = 12\, \text{V}$$
Voltage across 4 Ω: $$V = I \times R = 2 \times 4 = 8\, \text{V}$$
Note : 20V is divided among resistors.
Q
Draw the diagram of a circuit consisting of a battery of three cells of 2 V each, a 5 Ω resistor, an 8 Ω resistor and a 12 Ω resistor, and a plug key, all connected in series. Putting an ammeter to measure the current through the resistors and a voltmeter to measure the potential difference across the 12 Ω resistor. What would be the readings in the ammeter and the voltmeter ?
➤ Solution:
(a) Draw a Circuit Diagram
- Battery: 3 cells of 2 V each → Total Voltage = 3 x 2 = 6 V
- Resistors: 5 Ω, 8 Ω, 12 Ω
- Plug Key
(b) Add an Ammeter and Voltmeter
- Ammeter in series
- Voltmeter across the 12 Ω resistor in parallel

➤ Calculation:
- Total Resistance, R = 5 + 8 + 12 = 25 Ω
- Current flows throgh the circuit,
$$I = \frac{6}{25} = 0.24\, \text{A}$$
- Voltage across 12 Ω,
$$V = I \times R = 0.24 \times 12 = 2.88\, \text{V}$$
📌 Quick Revision Points
- Series combination: R = R₁ + R₂ + R₃ + …
- Same current in all resistors.
- Different voltage across each resistor.
- Used when higher resistance is required.
💡 Do You Know?
- Series resistors reduce current and increase voltage distribution.
- Series circuits are used in devices like decorative lights where the same current must flow through all components.
🔶 What is a Parallel Combination of Resistors?
When resistors are connected such that both ends of each resistor are connected to the same two points, they are said to be in parallel.
In such a case:
- The voltage (potential difference) across each resistor is the same.
- The total current is shared among the resistors.
📚 Law of Combination of Resistances in Parallel
According to this law:
The reciprocal of the total resistance is equal to the sum of the reciprocals of the individual resistances.
🔸 Formula:
If resistors R₁, R₂, R₃ are connected in parallel: $$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \ldots$$
🧠 Important Concepts to Remember
- Same voltage across all resistors.
- Different currents flow through each resistor.
- Total current (I) is the sum of individual currents:
$$I = I_1 + I_2 + I_3 + \ldots$$
- Resultant resistance (R) is always less than the smallest individual resistance in the parallel group.
📐 Derivation: Two Resistors in Parallel
Let resistors R₁ and R₂ be connected in parallel across a battery of V volts.

🔸 According to Ohm’s Law:
- Current through R₁: $$I_1 = \frac{V}{R_1}$$
- Current through R₂: $$I_2 = \frac{V}{R_2}$$
Total current supplied by the battery in the circuit: $$I = I_1 + I_2 = \frac{V}{R_1} + \frac{V}{R_2}$$
Let R be the equivalent resistance: $$I = \frac{V}{R}$$
Equating both expressions: $$\frac{V}{R} = \frac{V}{R_1} + \frac{V}{R_2}$$
Cancelling V: $$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}$$
📐 Derivation: Three Resistors in Parallel (Complete)
Let three resistors R₁, R₂, and R₃ be connected in parallel across a battery of V volts, as shown in the Figure.
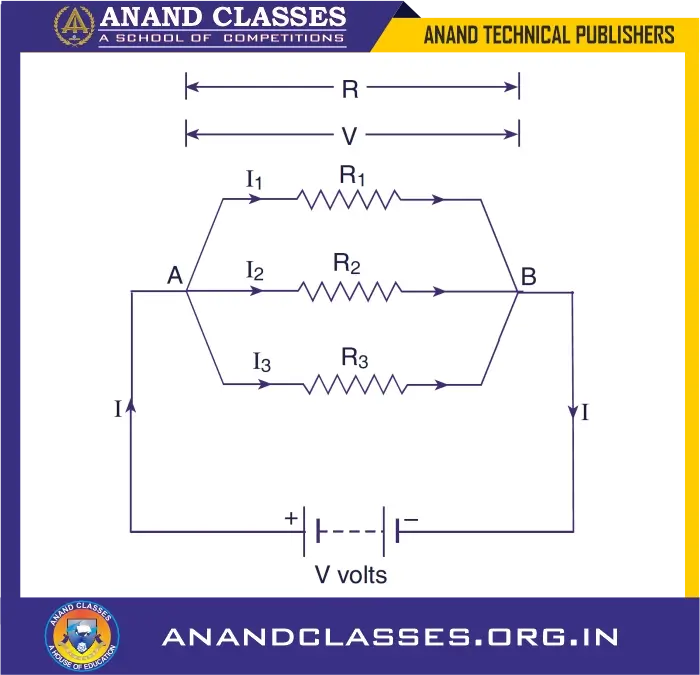
Since all resistors are connected between the same two points, the potential difference (V) across each of them is the same.
Let:
- Current through resistor R₁ = I₁
- Current through resistor R₂ = I₂
- Current through resistor R₃ = I₃
- Total current supplied by the battery = I
🔸 Using Ohm’s Law:
- For resistor R₁: $$I_1 = \frac{V}{R_1}$$
- For resistor R₂: $$I_2 = \frac{V}{R_2}$$
- For resistor R₃: $$I_3 = \frac{V}{R_3}$$
Now, total current in the circuit: $$I = I_1 + I_2 + I_3$$
Substitute the values of I₁, I₂, I₃: $$I = \frac{V}{R_1} + \frac{V}{R_2} + \frac{V}{R_3}$$
Let R be the equivalent resistance of the parallel combination. Then from Ohm’s law: $$I = \frac{V}{R}$$
Now equating both expressions for total current: $$\frac{V}{R} = \frac{V}{R_1} + \frac{V}{R_2} + \frac{V}{R_3}$$
Cancel V from both sides: $$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}$$
✅ Final Formula for Three Resistors in Parallel:
$$\boxed{ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} }$$
This formula can be extended to any number of resistors connected in parallel.
🧮 Numerical Examples
Q: Calculate the equivalent resistance when R₁ = 3 Ω and R₂ = 6 Ω are connected in parallel.
✅ Solution:

$$\frac{1}{R} = \frac{1}{3} + \frac{1}{6} = \frac{2 + 1}{6} = \frac{3}{6} \Rightarrow \frac{1}{R} = \frac{1}{2} \Rightarrow R = 2\, \Omega$$
Answer: The equivalent resistance is 2 ohms.
Q: Calculate the equivalent resistance when R₁ = 6 Ω and R₂ = 12 Ω are connected in parallel.
✅ Solution:
$$\frac{1}{R} = \frac{1}{6} + \frac{1}{12} = \frac{2 + 1}{12} = \frac{3}{12} $$
$$\frac{1}{R} = \frac{1}{4} \Rightarrow R = 4\, \Omega$$
Answer: The equivalent resistance is 4 ohms.
Q. In the circuit diagram shown alongside, the resistors $R_2$ and $R_3$ are connected in parallel, and their combination is connected in series with $R_1$. The battery provides a voltage of 6 V.
The values of the resistors are:
- $R_1 = 7.2\ \Omega$
- $R_2 = 8\ \Omega$
- $R_3 = 12\ \Omega$
🔍 Find:
- Total resistance of the circuit
- Total current flowing in the circuit
- Potential difference across the resistor $R_1$
✅ Solution:
Use Ohm’s Law and rules for series and parallel combination of resistances to solve this problem.

🌟 Given:
Three resistors:
- $R_1 = 7.2\ \Omega$
- $R_2 = 8\ \Omega$
- $R_3 = 12\ \Omega$
- Power supply:
$V = 6\ \text{volts}$
Resistors $R_2$ and $R_3$ are in parallel, and their combination is in series with $R_1$.
🧮 (i) Calculation of Total Resistance
👉 Step 1: Combine $R_2$ and $R_3$ (Parallel Combination)
In parallel, $$\frac{1}{R} = \frac{1}{R_2} + \frac{1}{R_3}$$
Substitute the values: $$\frac{1}{R} = \frac{1}{8} + \frac{1}{12}$$
$$\frac{1}{R} = \frac{3}{24} + \frac{2}{24} = \frac{5}{24}$$
$$R = \frac{24}{5} = 4.8\ \Omega$$
So, the equivalent resistance of $R_2$ and $R_3$ is 4.8 Ω.
👉 Step 2: Add $R_1$ in Series
Now, total resistance $$R_{total} = R_1 + R = 7.2 + 4.8 = 12\ \Omega$$
✅ Total resistance of the circuit = 12 ohms

⚡ (ii) Calculation of Total Current
We use Ohm’s Law: $$V = I \times R$$
$$I = \frac{V}{R} = \frac{6}{12} = 0.5\ \text{A}$$
✅ Total current = 0.5 amperes
Since it’s a series circuit, same current flows through all resistors, including R1R_1.
🔋 (iii) Calculation of Potential Difference across $R_1$
Using Ohm’s Law again: $$V = I \times R$$
$$V_{R_1} = 0.5 \times 7.2 = 3.6\ \text{V}$$
✅ Potential difference across $R_1 = 3.6\ \text{volts}$
🔁 Comparison: Series vs Parallel
| Feature | Series | Parallel |
|---|---|---|
| Voltage | Divided | Same across all |
| Current | Same through all | Divided |
| Total Resistance | Increases | Decreases |
| Formula | $R = R_1 + R_2 + \ldots$ | $\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \ldots$ |
📌 Quick Revision Points
- In parallel: $$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \ldots$$
- Voltage across all resistors = Battery Voltage
- Current splits based on resistance
- Total resistance is always less than the smallest resistor in parallel
💡 Do You Know?
- Parallel connections are used in household wiring so that each appliance gets full voltage and can work independently.
- Adding more resistors in parallel lowers the total resistance, allowing more current to flow.
🔍 FAQs on Series and Parallel Combination of Resistors
Q1. What is meant by resistors in series?
Ans. When resistors are connected end-to-end so that the same current flows through each, they are said to be in series.
Q2. What is meant by resistors in parallel?
Ans. When resistors are connected across the same two points, so that the voltage across each is the same, they are in parallel.
Q3. How is total resistance calculated in series?
Ans. In series:
$$R = R_1 + R_2 + R_3 + \dots$$
Q4. How is total resistance calculated in parallel?
Ans. In parallel: $$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots$$
Q5. What is the total resistance when two resistors of 6 Ω and 3 Ω are connected in series?
Ans. $$R = 6 + 3 = 9 \, \Omega$$
💡 Conceptual Questions with Answers
Q1. Why is the total resistance in parallel less than the smallest individual resistance?
Ans. Because parallel connections provide multiple paths for current, increasing total current flow and decreasing resistance.
Q2. If two identical resistors are connected (a) in series and (b) in parallel, in which case is the power consumed more?
Ans. In parallel, the power consumed is more because the equivalent resistance is lower, allowing more current to flow.
Q3. In which combination (series or parallel) does the potential difference divide?
Ans. In series, potential difference divides among the resistors.
✅ MCQs with Explanation
Q1. Three resistors of 2Ω, 3Ω, and 6Ω are connected in parallel. What is the total resistance?
A. 11Ω
B. 1Ω
C. 6Ω
D. 0.5Ω
Answer: B
Explanation: $$\frac{1}{R} = \frac{1}{2} + \frac{1}{3} + \frac{1}{6} = \frac{3 + 2 + 1}{6} = \frac{6}{6} = 1 \Rightarrow R = 1 \, \Omega$$
Q2. Which of the following remains the same in a parallel circuit?
A. Current
B. Voltage
C. Resistance
D. Power
Answer: B
Explanation: In parallel, all components get the same voltage.
Q3. What is the total resistance when three resistors 1Ω, 2Ω, and 3Ω are connected in series?
A. 1Ω
B. 6Ω
C. 5Ω
D. 0.5Ω
Answer: C
Explanation: In series, resistances add up:
$$R = 1 + 2 + 3 = 6 \, \Omega$$
Q4. Which statement is true for a series circuit?
A. Voltage across all resistors is the same
B. Current is divided in each resistor
C. Resistance is minimum
D. Same current flows through each resistor
Answer: D
Explanation: In series circuits, the same current flows through each resistor.
Q5. Which of the following is correct for resistors in parallel?
A. They have the same current
B. They have different voltages
C. They have the same voltage
D. They reduce current
Answer: C
Explanation: In a parallel circuit, all resistors are connected across the same two points, so the voltage across each is the same.
Q6. The equivalent resistance of two resistors connected in parallel is 4Ω. If one resistor is 8Ω, what is the value of the other?
A. 4Ω
B. 8Ω
C. 6Ω
D. 2Ω
Answer: A
Explanation: $$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}$$
$$\frac{1}{4} = \frac{1}{8} + \frac{1}{R_2}$$
$$\frac{1}{R_2} = \frac{1}{4} – \frac{1}{8} = \frac{1}{8} $$
$$R_2 = 8 \, \Omega$$
Q7. In a circuit, three resistors are connected in parallel. Which of the following quantities is different for all three resistors?
A. Voltage
B. Power
C. Resistance
D. Current
Answer: D
Explanation: The voltage is same in parallel, but current divides according to resistance.
🔄 Assertion and Reason Based MCQs
Q1.
Assertion (A): In series combination, the total resistance is more than any individual resistor.
Reason (R): In series, resistances add up directly.
A. Both A and R are true, and R is the correct explanation of A.
B. Both A and R are true, but R is not the correct explanation of A.
C. A is true but R is false.
D. A is false but R is true.
Answer: A
Q2.
Assertion (A): Parallel combination is preferred in household wiring.
Reason (R): It allows each appliance to receive the same voltage.
Answer: A
Explanation: Parallel connections keep voltage constant and ensure that the failure of one appliance doesn’t affect others.
Q3.
Assertion (A): The total resistance in a series circuit is greater than the highest individual resistance.
Reason (R): In series, resistances add directly.
A. Both A and R are true, and R is the correct explanation of A.
B. Both A and R are true, but R is not the correct explanation of A.
C. A is true but R is false.
D. A is false but R is true.
Answer: A
Q4.
Assertion (A): If one component fails in a series circuit, the entire circuit is broken.
Reason (R): In series circuits, current has only one path to flow.
Answer: A
Explanation: If the path is broken at any point in a series circuit, the current stops flowing.
Q5.
Assertion (A): All bulbs glow with the same brightness in a series circuit.
Reason (R): The voltage across each bulb is the same in series.
A. Both A and R are true, and R is the correct explanation of A.
B. Both A and R are true, but R is not the correct explanation of A.
C. A is true but R is false.
D. A is false but R is true.
Answer: C
Explanation: In series, current is the same, but voltage divides—so brightness may differ.
Q6.
Assertion (A): Total power consumed in a parallel circuit is the sum of powers consumed by each resistor.
Reason (R): In parallel, each resistor has different current but same voltage.
Answer: A
Explanation: P = VI
Since voltage is constant, the total power adds up.
📝 Worksheet: Practice Problems
Section A: Fill in the Blanks
- In a series circuit, the current is ________ through each resistor.
- Parallel circuits offer ________ resistance to current flow.
- Household electrical appliances are connected in ________.
Section B: Match the Following
| Column A | Column B |
|---|---|
| Series combination | Current same |
| Parallel combination | Voltage same |
| Low equivalent resistance | Parallel |
| High power consumption | Parallel |
Section C: Solve the Following
Q1. Find the equivalent resistance of three resistors 4Ω, 6Ω, and 12Ω connected in parallel.
Q2. Two resistors of 5Ω and 10Ω are connected in series. Find total resistance.
Q3. Which combination is best suited for home appliances and why?









