Learn about the position vector, its mathematical representation in 2D and 3D space, and how different observers perceive an object’s location. This guide includes FAQs, MCQs, conceptual questions, worksheets, test papers, and quick revision points for JEE, NEET, and CBSE Class 11.
Understanding Position with Multiple Observers
Any object occupies a definite point in space, but its position is perceived differently depending on the observer’s location. Consider an object placed at point O. Three different observers located at different positions will provide different descriptions of the position of point O. Each observer describes the position of point O in relation to themselves, and all observations are correct from their respective perspectives.
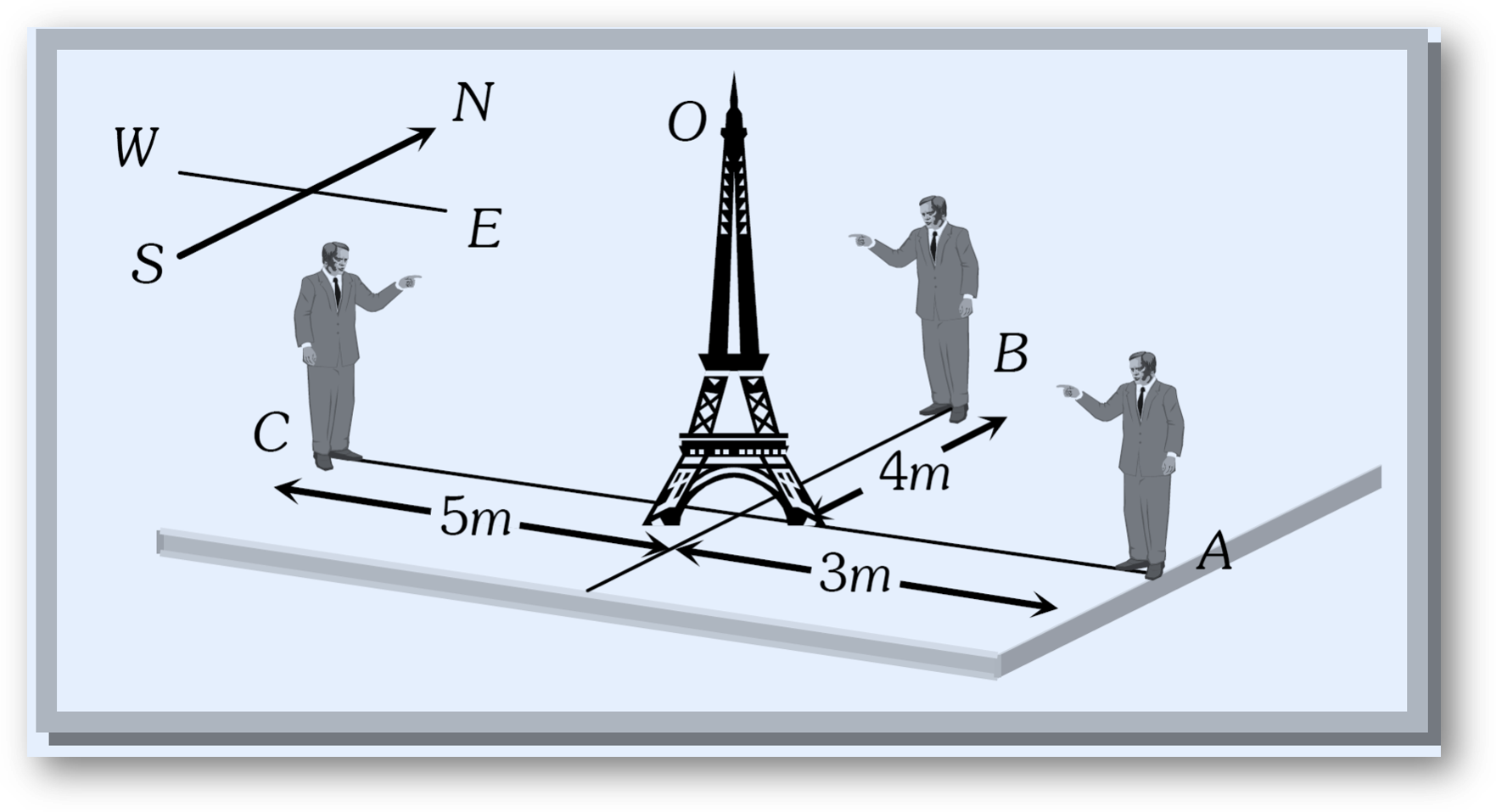
- Observer A: States that point O is 3 meters away in the west direction.
- Observer B: States that point O is 4 meters away in the south direction.
- Observer C: States that point O is 5 meters away in the east direction.
Thus, the position of any point is determined by two factors:
- Distance from the observer.
- Direction with respect to the observer.
To mathematically express the position of a point, we use a vector quantity called the position vector.
Position Vector Representation
If a point P is located in a two-dimensional plane with coordinates (x, y), then its position vector is given by: \begin{array}{l} \mathbf{r} = x \hat{i} + y \hat{j} \end{array}
If the point P is in three-dimensional space with coordinates (x, y, z), then the position vector is expressed as: \begin{array}{l} \mathbf{r} = x \hat{i} + y \hat{j} + z \hat{k} \end{array}
Here \begin{array}{l} \mathbf{} \hat{i} , \hat{j} , \hat{k} \end{array}
are unit vectors along the x, y, and z axes respectively.
Frequently Asked Questions (FAQs)
Q1: What is a position vector?
A1: A position vector is a vector that represents the position of a point relative to a reference origin.
Q2: Why do different observers report different positions for the same object?
A2: Different observers describe an object’s position relative to their own location, which leads to different observations. However, all observations are correct within their respective frames of reference.
Q3: Can position be negative?
A3: The magnitude of a position vector (distance) is always positive, but its components along the coordinate axes can be negative depending on the direction.
Q4: How does the position vector change with movement?
A4: If an object moves, its coordinates change, which in turn modifies its position vector.
Multiple-Choice Questions (MCQs)
Q1: A point has coordinates (3, 4). What is its position vector?
(a) 3i + 4j
(b) 4i + 3j
(c) 3j + 4i
(d) 7i + 1j
Answer: (a) 3i + 4j
Explanation: The position vector of a point (x, y) is given by xi+yj, so substituting x = 3 and y = 4, we get 3i + 4j.
Conceptual Questions
Q1: Can two observers see an object at the same location?
Answer: Yes, but only if they are positioned symmetrically with respect to the object or share the same frame of reference.
Q2: How does the coordinate system affect the position vector?
Answer: The position vector depends on the chosen coordinate system. A change in the origin or axis orientation alters the vector representation.
Do You Know?
- The position vector always originates from a reference point (usually the origin).
- The length (magnitude) of a position vector represents the actual distance from the reference point.
- Position vectors play a crucial role in kinematics and dynamics.
Worksheet
- Find the position vector of a point P(5, -3) in a 2D plane.
- A point is given by coordinates (-2, 4, 6). Write its position vector.
- If an object moves from (2, 3) to (5, 7), what is its displacement vector?
- Explain why position is a vector quantity.
Test Paper (10 Marks)
| Question | Marks |
|---|---|
| Define a position vector with an example. | 2 |
| Write the position vector for P(2, -3, 4). | 2 |
| A point moves from (1, 2) to (4, 6). Find the displacement vector. | 3 |
| Explain why different observers perceive different positions of the same object. | 3 |
Quick Revision Points
✅ Position depends on distance and direction.
✅ Position vector expresses location mathematically.
✅ In 2D: \begin{array}{l} \mathbf{r} = x \hat{i} + y \hat{j} \end{array}.
✅ In 3D: \begin{array}{l} \mathbf{r} = x \hat{i} + y \hat{j} + z \hat{k} \end{array}.
✅ Observers in different locations see different positions.
Best Coaching Center for IIT-JEE, NEET, and Foundations
ANAND CLASSES
📚 Buy complete study material at: Anand Classes Study Material
📞 Contact: +91-9463138669
📧 Email: anandclasses1996@gmail.com
Proprietor: “NIRMAL ANAND Educations”
Published by Anand Technical Publishers Under Anand Classes









