Introduction

Kepler’s Laws of Planetary Motion describe the movement of planets around the Sun. These laws were formulated by Johannes Kepler based on astronomical data collected by Tycho Brahe. They help in understanding celestial mechanics and the motion of planets in our solar system.

In astronomy, Kepler’s laws of planetary motion are three scientific laws describing the motion of planets around the sun.

Kepler’s first law – The law of orbits
Kepler’s second law – The law of equal areas
Kepler’s third law – The law of periods

Kepler’s First Law – The Law of Orbits

According to Kepler’s first law, “All the planets revolve around the sun in elliptical orbits having the sun at one of the foci”.

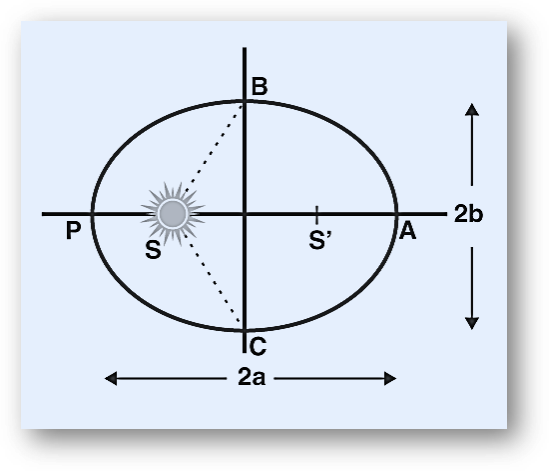
The point at which the planet is close to the sun is known as perihelion (about 147 million kilometres from the sun), and the point at which the planet is farther from the sun is known as aphelion (152 million kilometres from the sun). It is characteristic of an ellipse that the sum of the distances of any planet from two foci is constant.

Kepler’s Second Law – The Law of Equal Areas

Kepler’s second law states, “The radius vector drawn from the sun to the planet sweeps out equal areas in equal intervals of time”.

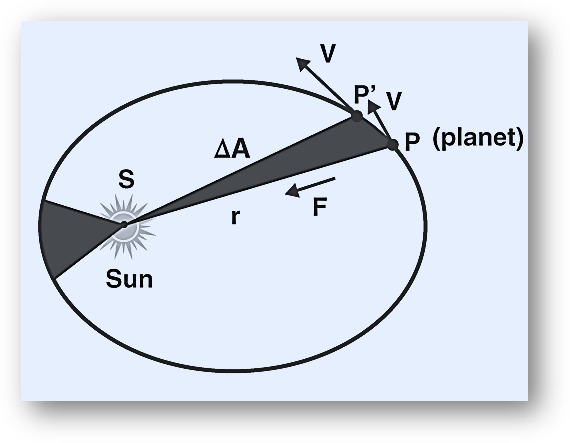
As the orbit is not circular, the planet’s kinetic energy is not constant in its path. It has more kinetic energy near the perihelion, and less kinetic energy near the aphelion implies more speed at the perihelion and less speed (v_min) at the aphelion. If r is the distance of the planet from the sun at perihelion (r_min) and at aphelion (r_max), then,

r_min+ r_max = 2a × (length of the major axis of an ellipse) . . . . . . . (1)

Using the law of conservation of angular momentum, the law can be verified. At any point of time, the angular momentum can be given as :

L = mr²ω

Now, consider a small area ΔA described in a short time interval Δt and the covered angle is Δθ. Let the radius of curvature of the path be r, then the length of the arc covered = r Δθ

ΔA = 1/2[r.(r.Δθ)]= 1/2r²Δθ

Therefore, ΔA/Δt = [ 1/2r²]Δθ/dt

Taking limits on both sides as, Δt→0, we get,

\(\begin{array}{l}\lim_{\Delta t\rightarrow 0}\frac{\Delta A}{\Delta t}=\lim_{\Delta t\rightarrow 0}\frac{1}{2}r^{2}\frac{\Delta \theta }{\Delta t}\end{array} \)

\(\begin{array}{l}\frac{dA}{dt}=\frac{1}{2}r^{2}\omega\end{array} \)

\(\begin{array}{l}\frac{dA}{dt}=\frac{L}{2m}\end{array} \)

Now, by conservation of angular momentum, L is a constant.

Thus, dA/dt = Constant

The area swept in equal intervals of time is a constant.

Kepler’s second law can also be stated as, “The areal velocity of a planet revolving around the sun in elliptical orbit remains constant, which implies the angular momentum of a planet remains constant”. As the angular momentum is constant, all planetary motions are planar motions, which is a direct consequence of central force.

Kepler’s Third Law – The Law of Periods

According to Kepler’s law of periods,”The square of the time period of revolution of a planet around the sun in an elliptical orbit is directly proportional to the cube of its semi-major axis”.

T² ∝ a³

The shorter the orbit of the planet around the sun, the shorter the time taken to complete one revolution. Using the equations of Newton’s law of gravitation and laws of motion, Kepler’s third law takes a more general form.

P²= 4π² /[G(M₁+ M₂)] × a³

Where M₁ and M₂ are the masses of the two orbiting objects in solar masses.

Kepler’s First Law: The Law of Ellipses-Q&A

Q: What is Kepler’s First Law?

A: Kepler’s First Law states that the orbit of a planet around the Sun is an ellipse, with the Sun at one of the two foci.

Q: What is an ellipse?

A: An ellipse is an elongated circle. It has two focal points, and the sum of the distances from any point on the ellipse to these foci remains constant.

Q: How does this law impact planetary motion?

A: It means that planets do not move in perfect circles but in slightly oval-shaped orbits, which explains why their distance from the Sun changes during their revolution.

Kepler’s Second Law: The Law of Equal Areas-Q&A

Q: What is Kepler’s Second Law?

A: Kepler’s Second Law states that a line joining a planet and the Sun sweeps out equal areas in equal time intervals.

Q: What does this law mean in practical terms?

A: It means that a planet moves faster when it is closer to the Sun (perihelion) and slower when it is farther from the Sun (aphelion).

Q: Why does this happen?

A: This is due to the conservation of angular momentum. When a planet is near the Sun, gravitational force pulls it strongly, increasing its speed. When it moves away, the force weakens, reducing its speed.

Kepler’s Third Law: The Law of Harmonies-Q&A

Q: What is Kepler’s Third Law?

A: Kepler’s Third Law states that the square of the orbital period (T) of a planet is proportional to the cube of the semi-major axis (r) of its orbit.

Mathematically, it is represented as: T² ∝ r³

Q: What does this law indicate?

A: It shows that planets farther from the Sun take longer to complete an orbit compared to those closer to the Sun.

Q: How is this law useful?

A: This law helps in calculating the distances of planets from the Sun and is crucial for predicting planetary motion.

Frequently Asked Questions (FAQs)

Q1: Do Kepler’s Laws apply only to our solar system?

A: No, Kepler’s Laws apply to all celestial bodies orbiting a central mass, including exoplanets and moons.

Q2: What is the significance of Kepler’s Laws in modern science?

A: These laws laid the foundation for Newton’s Law of Gravitation and are essential in space missions, satellite launches, and astronomy.

Q3: Why do planets move faster at perihelion and slower at aphelion?

A: Due to the conservation of angular momentum and the varying gravitational force exerted by the Sun.

Q4: Why are the orbits of the planets not circular?

A: For the orbits to be circular, it requires the planets to travel with a certain velocity, which is extremely unlikely. If there is any change in the velocity of the planet, the orbit will be elliptical.

MCQs with Answers and Explanations

1. According to Kepler’s First Law, the shape of a planetary orbit is:

a) Circular
b) Elliptical
c) Parabolic
d) Hyperbolic
Answer: (b) Elliptical
Explanation: Planets move in elliptical orbits with the Sun at one focus, as per Kepler’s First Law.

2. Kepler’s Second Law states that a planet moves faster when:

a) It is far from the Sun
b) It is near the Sun
c) It moves in a straight line
d) It is stationary
Answer: (b) It is near the Sun
Explanation: Planets move faster at perihelion due to stronger gravitational pull.

3. Kepler’s Third Law relates:

a) Orbital speed and mass of the planet
b) Orbital period and distance from the Sun
c) Temperature and size of the planet
d) Gravity and motion of Earth
Answer: (b) Orbital period and distance from the Sun
Explanation: The square of the orbital period is proportional to the cube of the semi-major axis of the orbit.

Test Your Knowledge

Kepler’s Laws Quiz

Conclusion

Kepler’s Laws of Planetary Motion are fundamental in understanding the motion of celestial bodies. They explain why planets move in elliptical orbits, how their speed varies, and how their distance from the Sun affects their revolution. These laws remain crucial in astronomy, astrophysics, and space exploration.

Buy Complete Study Material for JEE, NEET & CBSE Board Class 11 Exams

Get in-depth study material for Physics, Chemistry, Mathematics, and Biology at https://publishers.anandclasses.co.in/ to excel in JEE, NEET, and CBSE Board Exams.

Proprietor: NIRMAL ANAND Educations
Written by: Neeraj Anand
Published by: Anand Technical Publishers Under Anand Classes
Contact: +91-9463138669
Email: anandclasses1996@gmail.com