Effects on Acceleration Due to Gravity (g) with Height (h) | Gravitation Class 11 Physics Notes, Important Questions & Answers, MCQS, Quiz

The Variation of g with Height (h)

Consider an object P (of mass m) at a height h from the surface of the earth, R be the radius of the earth as shown in the figure below:

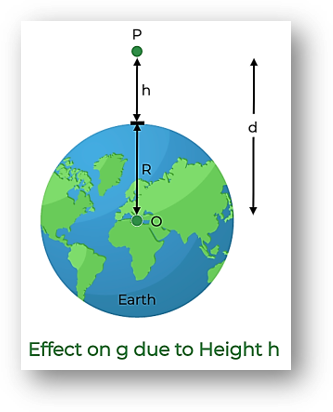
The gravitational force F acting on the mass m at height (h) from surface of earth is,

F = GMm/ (R+h)²

where, M is the mass of the Earth.

Since, F = mg_h, where g_h is the acceleration due to gravity at height h. Then the above equation becomes:

mg_h = GMm/(R+h)²

g_h = GM/R² (1+h/R)²     

g_h = (GM/R²)/(1+h/R)²

Since, g = GM/R²

Therefore, 

g_h = g/(1+h/R)²

Approximation Formula:

g_h = g (1+h/R)^–2

Now, if h is much lesser than the radius of the earth i.e. when h << R, then according to Binomial Theorem, the value of g at height h is given by:

g_h = g (1 – 2h/R)

Important Conclusion on Acceleration Due to Gravity : For an object placed at a height of h, the acceleration due to gravity is less as compared to that placed on the surface.

Effect of Altitude :  When a body moves away from the surface of the earth the force of attraction decreases as the distance between the earth and the body increases.

Example 1 :

A person weighs 50 kg on Earth. On the surface of Neptune, where the acceleration of gravity is approximately 1.2 times as great as that on Earth, what will be the person’s mass?

Solution: 

The person will weigh 50 kg on the surface of Neptune because the force of gravity changes the weight of the object and not it’s mass. The mass of an object stays constant regardless of the forces acting upon it.

Example 2:

It has been noted that at a place above the earth’s surface, the value of g is 0.2 m/s². Determine this height above the earth’s surface at which the given g is obtained. 

Solution:

Consider the height above earth surface be h’. 

Therefore,

g_h = g (1− 2h / R)

or ​

g_h / g = (1− 2h / R)

Substitute the given values in the above expression as,

0.2 m/s² / 9.8 m/s² = (1− 2h / R)

2h / R = 48 / 49

h = 3134. 7 km 

= 3134.7 km

Important Questions & Answers on Effects on Acceleration Due to Gravity (g) with Height (h)

Q1: What is acceleration due to gravity (g)?

A: Acceleration due to gravity (g) is the acceleration experienced by an object due to the gravitational pull of the Earth. Its standard value on the Earth’s surface is 9.8 m/s².

Q2: How does the value of g change with height (h)?

A: The value of g decreases as we move above the Earth’s surface (increase in height h). This happens because gravity weakens with distance from the Earth’s center.

Q3: What is the mathematical expression for g at a height h?

A: The formula to calculate the acceleration due to gravity at height h is:

g_h = g/(1+h/R)²

Where:

• g_h = Acceleration due to gravity at height h
• g = Acceleration due to gravity on Earth’s surface (9.8 m/s²)
• R = Radius of Earth (~6400 km)
• h = Height above the Earth’s surface

Q4: What happens to g when h << R (h is very small compared to R)?

A: When h is much smaller than R, we can use an approximate formula:

g_h = g (1 – 2h/R)

This approximation shows that g decreases linearly with a small increase in height.

Q5: Why does g decrease with height?

A: Gravity follows the inverse square law, meaning that as distance from the Earth’s center increases, gravitational force decreases proportionally to the square of the distance.

FAQs on Effects of Height on g

Q1: Does g become zero at a certain height?

A: No, g never becomes zero. However, it continues to decrease with height and becomes extremely small at large distances from Earth.

Q2: What happens to the weight of an object at a high altitude?

A: Since weight is given by W=mg_h, and g_h decreases with height, an object’s weight reduces as altitude increases.

Q3: How does the variation of g with height affect satellite motion?

A: Satellites orbit the Earth at high altitudes where g is weaker. Their motion follows circular or elliptical orbits due to the balance between gravity and centripetal force.

MCQs on Variation of g with Height

Q1: If the radius of Earth is 6400 km, what will be the approximate value of g at 100 km above the surface?

A) 9.8 m/s²
B) 9.5 m/s²
C) 8.7 m/s²
D) 7.2 m/s²

Answer: B
Explanation: Using the formula g_h = g/(1+h/R)², we get an approximate value of 9.5 m/s² at h = 100 km altitude with R = 6400 km (radius of earth).

Q2: What happens to an astronaut’s weight as they move away from the Earth?

A) Increases
B) Decreases
C) Remains constant
D) Becomes zero instantly

Answer: B
Explanation: Since weight is directly proportional to g, as g decreases with height, the astronaut’s weight also decreases.

Test Your Knowledge

Buy Complete Study Material at:

🔗 Anand Classes Study Material

Proprietor: NIRMAL ANAND Educations
Written by: Neeraj Anand
Published by: Anand Technical Publishers Under Anand Classes
📞 Contact: +91-9463138669
✉️ Email: anandclasses1996@gmail.com