In everyday language, the words distance and displacement are used in the same sense but in physics these two words have different meanings. Let us understand this difference by taking with an example as follows.
Understand Distance Travelled and Displacement
Imagine a man who lives at Point A and needs to reach Point C. However, before reaching C, he must meet his friend at Point B. He starts from A, travels 5 km to B, and then continues for 3 km to C. The total path he follows, ABC, represents the actual distance traveled, which is 8 km.
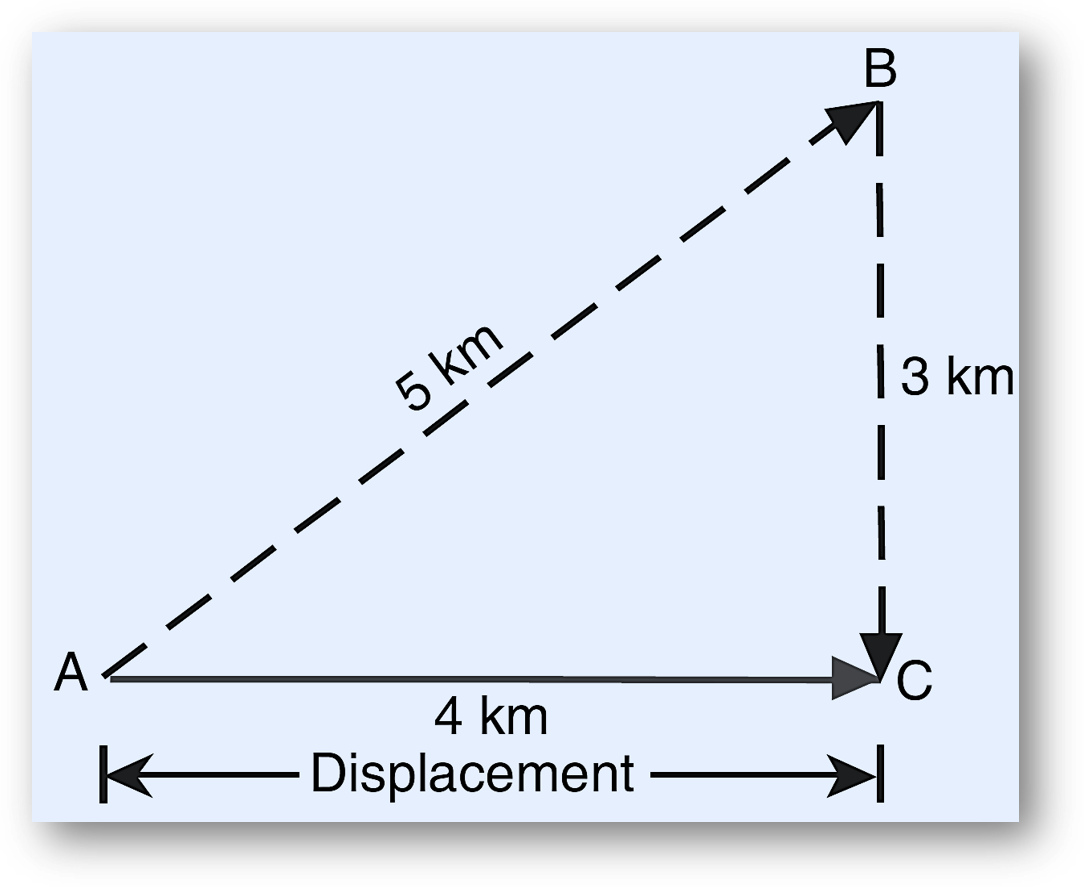
Displacement = 4 km towards East.
Understanding Distance
The distance traveled by a moving body is the actual length of the path covered, regardless of direction. In this case:
📏 Total Distance = 5 km + 3 km = 8 km
Understanding Displacement
Now, let’s analyze the shortest route. Instead of following the indirect path ABC, we draw a straight line from A to C, measuring 4 km. This straight-line distance (AC) is called displacement. It tells us how far the man is from his starting point, along with direction.
AB2 = AC2 + BC2
AC2 = AB2 – BC2
AC2 = 52 – 32
AC = 4 km
🧭 Displacement = 4 km (East direction)
📌 Key Difference:
- Distance is the total path covered (8 km).
- Displacement is the shortest straight-line distance between the start and end points (4 km, East).
Distance vs. Displacement: A Clear Distinction
💡 When a body moves from one position to another:
- Distance refers to the actual path traveled.
- Displacement refers to the shortest straight-line path between the initial and final positions.
📍 Definition of Displacement: When a body moves from one point to another, the shortest (straight-line) distance between the initial position and final position, along with direction, is called displacement.
Scalar and Vector Quantities
Physical quantities like distance and displacement are fundamental concepts in physics. They can be classified as scalars or vectors:
✅ Scalar Quantity:
- Has magnitude only (size or numerical value)
- ❌ No direction
- Example: Distance (e.g., “50 km”)
✅ Vector Quantity:
- Has both magnitude and direction
- ✔ Direction matters!
- Example: Displacement (e.g., “50 km towards East”)
Can Distance Be Zero? Can Displacement Be Zero?
🚶 Distance can never be zero as long as the body moves.
⚡ Displacement can be zero if the body returns to its starting point.
Following two examples where a body travels a certain distance but the final displacement of the body is zero.
Example:
A man travels: 1️⃣ 5 km from A to B 2️⃣ 3 km from B to C 3️⃣ 4 km from C back to A
📏 Total Distance = 5 km + 3 km + 4 km = 12 km
🧭 Final Displacement = 0 km (since he is back at A)
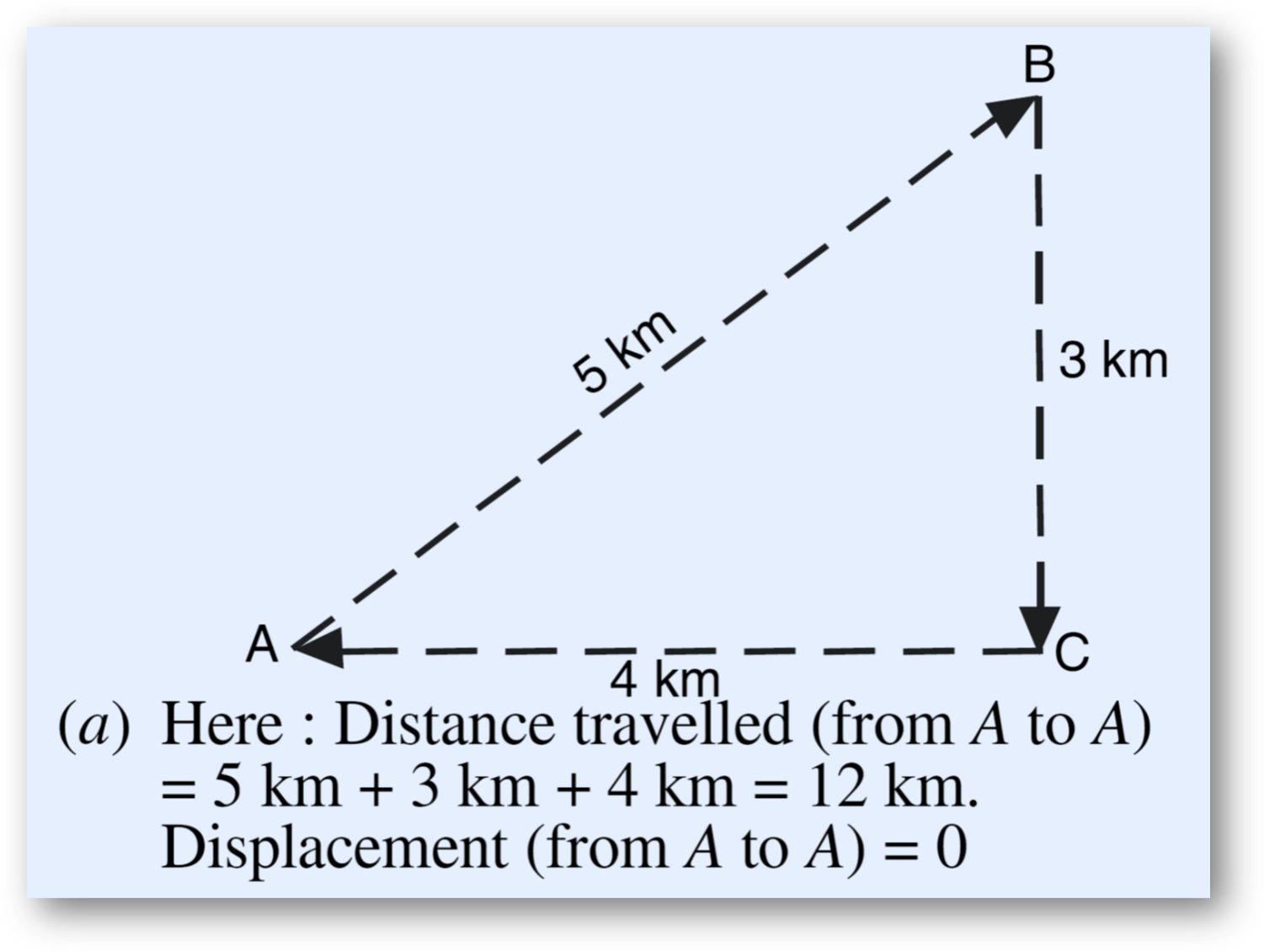
🌀 Conclusion:
- If we take a round trip and return to the starting point, distance remains measurable, but displacement is zero.
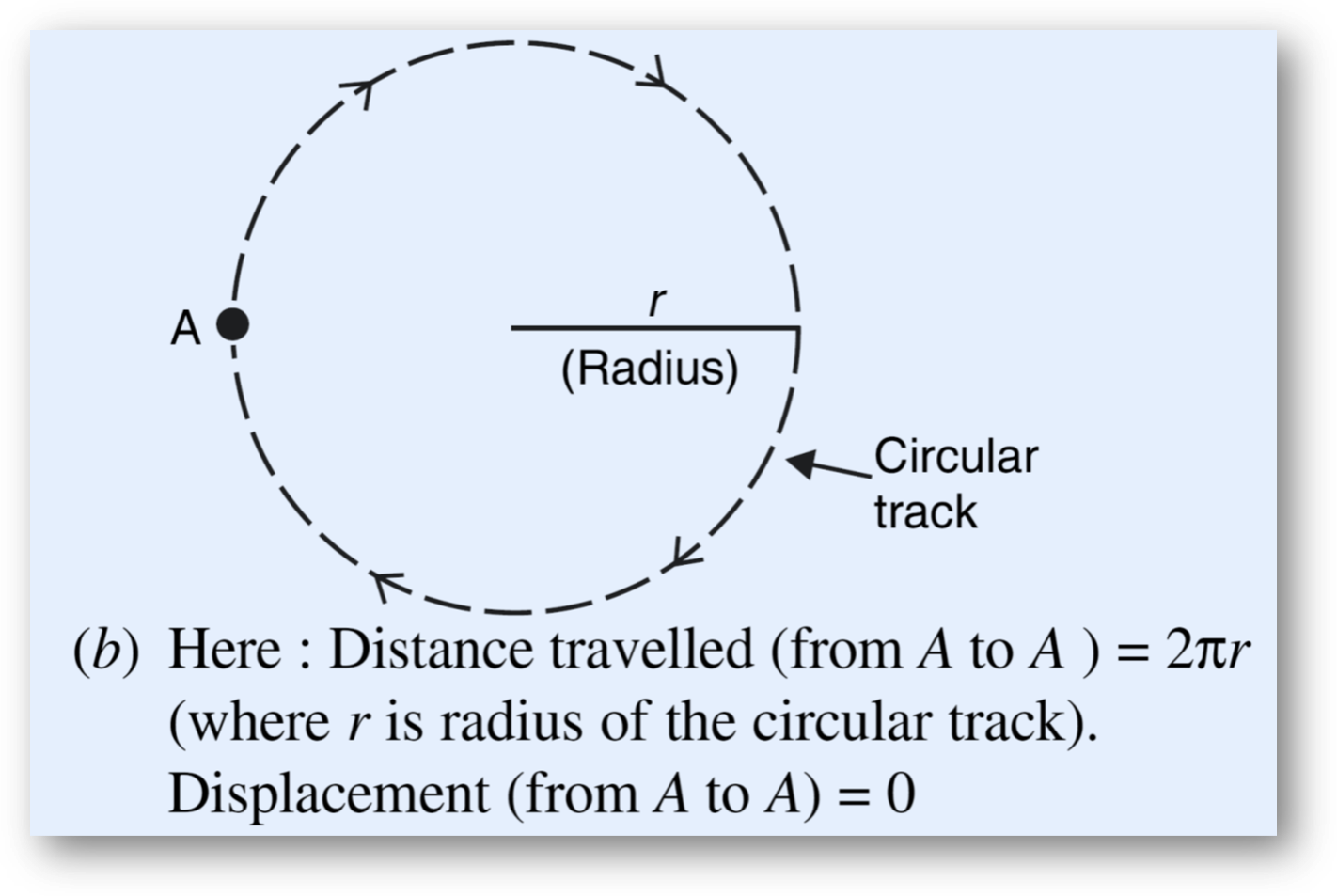
- Example: Completing one full lap on a circular track → Distance = Circumference = 2πr, Displacement = 0.
🔹 Distance: Total path traveled
🔹 Displacement: Shortest path between start and end points (with direction!)
Question-Answer Format for Exams
Conceptual Questions
- What is the difference between distance and displacement?
- Answer: Distance is the total length of the path traveled, while displacement is the shortest distance from the start to end point, considering direction.
- Can displacement be greater than distance?
- Answer: No, displacement is always equal to or smaller than distance.
- Why is displacement a vector quantity?
- Answer: Because it has both magnitude and direction.
- Give an example where displacement is zero but distance is not.
- Answer: If a person walks around a circular track and returns to the starting point, displacement is zero but distance is the entire circumference traveled.
Multiple Choice Questions (MCQs)
- A car moves 10 km North, then 10 km South. What is the displacement?
- (a) 20 km
- (b) 10 km
- (c) 0 km ✅
- (d) 5 km
- Explanation: Since the car returns to its starting point, the shortest distance (displacement) is zero.
- Which of the following is a vector quantity?
- (a) Distance
- (b) Speed
- (c) Displacement ✅
- (d) Time
- Explanation: Displacement has both magnitude and direction.
- A body moves from A to B covering 6 km and returns to A. What is the displacement?
- (a) 12 km
- (b) 6 km
- (c) 0 km ✅
- (d) Cannot be determined
- Explanation: The initial and final positions are the same, so displacement is zero.
Do You Know?
- Displacement is always a straight line, but distance is the path taken.
- Distance can be greater than displacement, but never less.
- Displacement can be zero even if distance is nonzero.
- Displacement is used in physics equations, while distance is used for daily measurements.
Worksheet
- A person moves 4 km North, 3 km East, and 4 km South. Calculate distance and displacement.
- A car travels 5 km North, 5 km East, and then 5 km South. Find the distance and displacement.
- A cyclist moves in a circular path of radius 10 m and completes one round. Calculate the distance and displacement.
- What type of quantity is:
- (a) Distance?
- (b) Displacement?
- A train moves 60 km East and 80 km North. Find the displacement using the Pythagorean theorem.
Test Paper (Marks Distribution)
Total Marks: 14
- Define distance and displacement with an example. (2 marks)
- State whether the following are scalars or vectors: speed, velocity, distance, displacement. (2 marks)
- A person walks 3 km North, then 4 km East. Find the displacement. (4 marks)
- Explain why displacement can be zero even when distance is not. (2 marks)
- Solve: A car moves 5 km West and then 12 km North. Find its displacement. (4 marks)
Important Points for Quick Revision
✅ Distance is a scalar, displacement is a vector.
✅ Displacement can be zero even if distance is not.
✅ Distance is the total path covered, displacement is the shortest path.
✅ If final and initial positions are the same, displacement = 0.
✅ Displacement can never be greater than distance.
✅ SI Unit for both is meters (m).
Best Coaching Center for IIT-JEE, NEET, and Foundations – ANAND CLASSES
Buy complete study material at: https://publishers.anandclasses.co.in/
Proprietor: NIRMAL ANAND Educations
Written by: Neeraj Anand
Published by: Anand Technical Publishers Under Anand Classes
📞 Contact: +91-9463138669
📧 Email: anandclasses1996@gmail.com









